题目内容
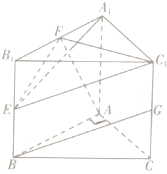 已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.
已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:根据条件以A为坐标原点,以AB,AC,AA1分别x,y,z轴建立空间坐标系,利用坐标法进行证明即可.
解答:
证明:∵AA1⊥底面ABC,∠BAC=90°
∴建立以A为坐标原点,以AB,AC,AA1分别x,y,z轴建立空间坐标系如图: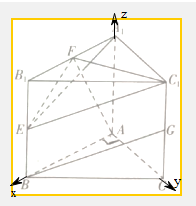
∵AA1=AC=AB,
∴设AA1=AC=AB=1,
则B(1,0,0),C(0,1,0),A1(0,0,1),B1(1,0,1),C1(0,1,1),
∵点E,F,G分别是棱BB1,A1B1,CC1的中点,
∴F(
,0,1),G(0,1,
),
则
=(
,0,1),
=(-1,1,
),
则
•
=(
,0,1)•(-1,1,
)=-
+
=0,
则
⊥
,即AF⊥BG
∴建立以A为坐标原点,以AB,AC,AA1分别x,y,z轴建立空间坐标系如图:

∵AA1=AC=AB,
∴设AA1=AC=AB=1,
则B(1,0,0),C(0,1,0),A1(0,0,1),B1(1,0,1),C1(0,1,1),
∵点E,F,G分别是棱BB1,A1B1,CC1的中点,
∴F(
| 1 |
| 2 |
| 1 |
| 2 |
则
| AF |
| 1 |
| 2 |
| BG |
| 1 |
| 2 |
则
| AF |
| BG |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则
| AF |
| BG |
点评:本题主要考查空间直线垂直的判断,建立坐标系利用向量法是解决本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
已知抛物线x2=2py(p>0)的焦点为F,A,B,C都是抛物线上的点,满足
+
+
=
,则kAB+kBC+kAC=( )
| FA |
| FB |
| FC |
| 0 |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、不能确定 |
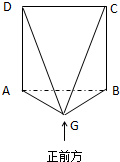 如图,四棱锥G-ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG.
如图,四棱锥G-ABCD中,ABCD是正方形,且边长为2a,面ABCD⊥面ABG,AG=BG.