Question

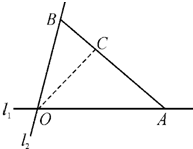如图，在C城周边已有两条公路l₁，l₂在点O处交汇，且它们的夹角为75°．已知OC=（

2

+

6

） km，OC与公路l₁的夹角为45°．现规划在公路l₁，l₂上分别选择A，B两处为交汇点（异于点O）直接修建一条公路通过C城．设OA=x km，OB=y km．
（1）求y关于x的函数解析式，并指出它的定义域；
（2）试确定点A，B的位置，使△OAB的面积最小．

Answer 1

考点：在实际问题中建立三角函数模型

专题：应用题,三角函数的图像与性质

分析：（1）由△AOC的面积与△BOC的面积之和等于△AOB的面积可得

1

2

x（

2

+

6

）sin45°+

1

2

y（

2

+

6

）sin30°=

1

2

xysin75°，从而求得y=

2 2 x

x-2

（x＞2）．
（2）△AOB的面积S=

1

2

xysin75°=

3 +1

2

•（（x-2）+

4

x-2

+4）；利用基本不等式求最值．

解答： 解：（1）因为△AOC的面积与△BOC的面积之和等于△AOB的面积，
所以

1

2

x（

2

+

6

）sin45°+

1

2

y（

2

+

6

）sin30°=

1

2

xysin75°，
即

2

2

x（

2

+

6

）+

1

2

y（

2

+

6

）=

6 + 2

4

xy，
所以y=

2 2 x

x-2

（x＞2）．
（2）△AOB的面积S=

1

2

xysin75°
=

1

2

•x•

2 2 x

x-2

•sin75°
=

3 +1

2

•

x2

x-2

=

3 +1

2

•（（x-2）+

4

x-2

+4）
≥

3 +1

2

×8=4（

3

+1），
当且仅当x-2=

4

x-2

，即x=4时取等号，
此时y=

2 2 ×4

4-2

=4

2

．
故当OA=4km，OB=4

2

 km时，△OAB的面积最小，最小值为4（

3

+1）km²．

点评：本题考查了函数在实际问题中的应用，同时考查了基本不等式，属于中档题．