题目内容
19.已知全集为R,A={x|$lo{g}_{\frac{1}{2}}$(3-x)≥-2},B={x|-2<x≤3},求(∁RA)∩B.分析 先求出集合A,进而求出CRA,由此能求出(∁RA)∩B.
解答 解:∵全集为R,A={x|$lo{g}_{\frac{1}{2}}$(3-x)≥-2}={x|$\left\{\begin{array}{l}{3-x>0}\\{3-x<4}\end{array}\right.$}={x|-1<x<3},
B={x|-2<x≤3},
∴(∁RA)∩B{x|x≤-1或x≥3}∩{x|-2<x≤3}={x|-2<x<-1或x≥3}.
点评 本题考查交集、补集的求法,是基础题,解题时要认真审题,注意对数函数性质的合理运用.

练习册系列答案
相关题目
3.已知关于x的方程4x+m•2x+m2-1=0有实根,则实数m的取值范围是( )
| A. | [-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$] | B. | [-$\frac{2\sqrt{3}}{3}$,1) | C. | [-$\frac{2\sqrt{3}}{3}$,1] | D. | [1,$\frac{2\sqrt{3}}{3}$] |
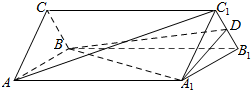 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.