题目内容
10.几何体的三视图如图所示,则该几何体的体积为$\frac{10}{3}$.
分析 由已知中的三视图,得该几何体是一个三棱柱切去一个三棱锥所得的几何体,分别计算出柱体和锥体的体积,相减可得答案.
解答 解:根据几何体的三视图,得该几何体是一个三棱柱切去一个三棱锥所得的几何体,
三棱柱的体积为:$\frac{1}{2}$×2×2×2=4,
三棱锥的体积:$\frac{1}{3}$×$\frac{1}{2}$×2×2×(2-1)=$\frac{2}{3}$,
故组合体的体积V=4-$\frac{2}{3}$=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题考查了由三视图求体积的应用问题,根据三视图判断出几何体的形状是解题的关键.

练习册系列答案
相关题目
1.已知函数$f(x)=tan({2x+\frac{π}{3}})$,则$f({\frac{25π}{6}})$=( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
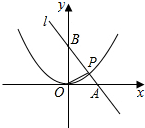 如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内交于P点,如果△AOP的面积为2,求此抛物线的解析式.
如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内交于P点,如果△AOP的面积为2,求此抛物线的解析式.