题目内容
7.一艘轮船从码头出发驶向河对岸,已知轮船的速度为6km/h,河水的流速为2km/h,轮船的实际航行路线与对岸的岸边垂直.(1)试用向量表示河水速度、轮渡速度以及轮渡实际航行的速度;
(2)求轮船航行的实际速度的大小(精确到0.01,参考数据$\sqrt{2}$≈1.414).
分析 (1)设河水速度为$\overrightarrow{{v}_{0}}$、轮渡速度为$\overrightarrow{{v}_{1}}$,轮渡实际航行的速度为$\overrightarrow{v}$,由题意能用向量表示河水速度、轮渡速度以及轮渡实际航行的速度.
(2)由$\overrightarrow{{v}_{1}}=6$km/h,$\overrightarrow{{v}_{0}}$=km/h,$\overrightarrow{v}⊥\overrightarrow{{v}_{0}}$,利用勾股定理能求出轮船航行的实际速度.
解答 解:(1)设河水速度为$\overrightarrow{{v}_{0}}$、轮渡速度为$\overrightarrow{{v}_{1}}$,轮渡实际航行的速度为$\overrightarrow{v}$,
由题意用向量表示河水速度、轮渡速度以及轮渡实际航行的速度如下图: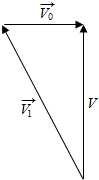
(2)∵$\overrightarrow{{v}_{1}}=6$km/h,$\overrightarrow{{v}_{0}}$=km/h,$\overrightarrow{v}⊥\overrightarrow{{v}_{0}}$,
∴轮船航行的实际速度$\overrightarrow{v}$=$\sqrt{{6}^{2}-{2}^{2}}$=$\sqrt{32}$=4$\sqrt{2}$≈5.656(km/h).
点评 本题考查向量表示河水速度、轮渡速度以及轮渡实际航行的速度,考查轮船航行的实际速度的大小的求法,是基础题,解题时要注意向量三角形法则的合理运用.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
16.若向量$\overrightarrow{a}$=(2,3,λ),$\overrightarrow{b}$=(-1,1,$\frac{\sqrt{6}}{3}$)的夹角为60°,则λ等于( )
| A. | $\frac{23}{12}$ | B. | $\frac{\sqrt{6}}{12}$ | C. | $\frac{23\sqrt{6}}{12}$ | D. | -$\frac{23\sqrt{6}}{12}$ |
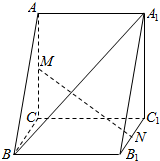 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.