题目内容
9.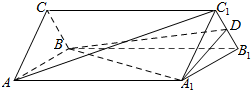 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,各棱长均为2,D为线段B1C1中点.(Ⅰ) 证明:AC1∥平面A1BD;
(Ⅱ) 求BB1与平面A1BD所成角的正弦值.
分析 (Ⅰ)连接AB1,交A1B于点F,连接DF,则DF∥AC1,由此能证明AC1∥平面A1BD.
(Ⅱ)解法1:作B1H⊥BD,垂足为H,推导出A1D⊥平面BB1C1C,从而B1H⊥A1D,进而∠B1BH为BB1与平面A1BD所成的角,由此能求出BB1与平面A1BD所成角的正弦值.
解法2:取AB中点O,连接CO,以O为原点,建立空间直角坐标系O-xyz,利用向量法能求出BB1与平面A1BD所成角的正弦值.
解答  (本小题满分12分)
(本小题满分12分)
证明:(Ⅰ)连接AB1,交A1B于点F,
连接DF,△AB1C1中,D,F分别为A1B,B1C1中点,
所以DF∥AC1.…(2分)
因为DF?平面A1BD,AC1?平面A1BD
所以AC1∥平面A1BD. …(4分)
解:(Ⅱ)方法1:如图,作B1H⊥BD,垂足为H,
因为BB1⊥平面A1B1C1,A1D?平面A1B1C1,所以A1D⊥BB1,
又A1D⊥B1C1,且BB1∩B1C1=B1,BB1,B1C1?平面BB1C1C,
所以A1D⊥平面BB1C1C.…(6分)
因为B1H?平面BB1C1C,所以B1H⊥A1D,
又B1H⊥BD,且A1D∩BD=D,A1D,BD?平面A1BD,
所以B1H⊥平面A1BD,所以∠B1BH为BB1与平面A1BD所成的角.…(8分)
在Rt△B1BD中,$sin∠{B_1}BH=\frac{{{B_1}D}}{BD}=\frac{{\sqrt{5}}}{5}$.…(11分)
因此BB1与平面A1BD所成角的正弦值为$\frac{{\sqrt{5}}}{5}$.…(12分)
方法2:取AB中点O,连接CO.
因为AA1⊥平面ABC,CO?平面ABC,所以CO⊥AA1.
又因为CO⊥AB,且AA1∩AB=A,AA1,AB?面A1ABB1,所以,CO⊥平面A1ABB1.…(6分)
如图,以O为原点,建立空间直角坐标系O-xyz如图所示,
则A1(1,2,0),B(-1,0,0),B1(-1,2,0),$D({-\frac{1}{2},2,\sqrt{3}})$,
所以,$\overrightarrow{B{A_1}}=({2,2,0})$,$\overrightarrow{BD}=({\frac{1}{2},2,\frac{{\sqrt{3}}}{2}})$,
$\overrightarrow{B{B_1}}=({0,2,0})$.…(8分)
设平面A1BD的法向量$\overrightarrow{n}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{B{A}_{1}}=0}\\{\overrightarrow{n}•\overrightarrow{BD}=0}\end{array}\right.$,得$\left\{\begin{array}{l}2x+2y=0\\ \frac{1}{2}x+2y+\frac{{\sqrt{3}}}{2}z=0\end{array}\right.$,
解得$\left\{\begin{array}{l}y=-x\\ z=\sqrt{3}x\end{array}\right.$,
令x=1,得$\overrightarrow{n}$=(1,-1,$\sqrt{3}$),…(10分)
设直线BB1与平面A1BD所成角大小为θ,
则sinθ=|$cos<\overrightarrow{n},\overrightarrow{B{B}_{1}}>$|=$\frac{|\overrightarrow{n}•\overrightarrow{B{B}_{1}}|}{|\overrightarrow{n}|•|\overrightarrow{B{B}_{1}}|}$=$\frac{\sqrt{5}}{5}$,
所以,BB1与平面A1BD所成角的正弦值为$\frac{{\sqrt{5}}}{5}$.…(12分)
点评 本题考查线面平行的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

| A. | (-∞,1) | B. | (-2,6) | C. | [-2,6] | D. | {-2,6} |
| A. | $\frac{256π}{81}$ | B. | $\frac{64π}{27}$ | C. | $\frac{16π}{9}$ | D. | $\frac{4π}{3}$ |
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
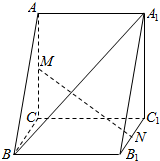 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.