题目内容
8．有5名男生4名女生，全体排成一排，问下列情形各有多少种不同的排法？（1）男生甲站左端；
（2）男生甲站中间；
（3）两端都是男生；
（4）两端不都是男生．
分析 （1）（2），先排甲有1种，剩下的8个元素全排列有A88种，根据分步计数原理得到结果．
（3）先排两端，再排其余7人，再根据分步计数原理得到结果．
（4）利用间接法求解．
解答 解：（1）男生甲站左端，有A88=40320种排法；
（2）男生甲站中间，有A88=40320种排法；
（3）两端都是男生，有A52A77=100800种排法；
（4）两端不都是男生，有A99-A52A77=383040种排法．
点评 本题集排列多种类型于一题，充分体现了元素分析法（优先考虑特殊元素）、位置分析法（优先考虑特殊位置）、直接法、间接法（排除法）等常见的解题思路．
练习册系列答案
相关题目
16．若向量$\overrightarrow{a}$=（2，3，λ），$\overrightarrow{b}$=（-1，1，$\frac{\sqrt{6}}{3}$）的夹角为60°，则λ等于（ ）
| A． | $\frac{23}{12}$ | B． | $\frac{\sqrt{6}}{12}$ | C． | $\frac{23\sqrt{6}}{12}$ | D． | -$\frac{23\sqrt{6}}{12}$ |
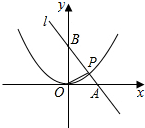如图，直线l经过A（4，0）和B（0，4）两点，它与抛物线y=ax2在第一象限内交于P点，如果△AOP的面积为2，求此抛物线的解析式．