题目内容
长度为1的线段AB(B在A的右边)在x轴上移动,点P(0,1)与A点连成直线PA,点Q(1,2)与B点连成直线QB,求直线PA和直线QB交点M的轨迹方程.
考点:轨迹方程
专题:综合题
分析:由题意画出图形,设出M,A,B的坐标,分A在原点和不在原点讨论,当A不在原点时,分别求出直线PA和直线QB的方程,求出交点,消掉参数后得答案.
解答:
解:如图,

设交点M(x,y),A(a,0),B(a+1,0),
(1)当a不为0时,由直线方程的截距式并化简得直线AP的方程为:y=-
x+1 ①,
由直线方程的两点式并化简求出直线BQ的方程:y=-
( x-a-1 ) ②,
联立①②得,
,消掉参数a得:xy-2y+2=0;
(2)当a为0时,直线PA和直线QB没有交点,两条线平行.

设交点M(x,y),A(a,0),B(a+1,0),
(1)当a不为0时,由直线方程的截距式并化简得直线AP的方程为:y=-
| 1 |
| a |
由直线方程的两点式并化简求出直线BQ的方程:y=-
| 2 |
| a |
联立①②得,
|
(2)当a为0时,直线PA和直线QB没有交点,两条线平行.
点评:本题考查了轨迹方程的求法,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
给出下列命题:
①底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
②若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
③一个棱锥可以有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱一定是正方体.
其中正确的命题是( )
①底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
②若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
③一个棱锥可以有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱一定是正方体.
其中正确的命题是( )
| A、①②③ | B、①③ | C、②③④ | D、④ |
已知a>0,b>0,3是3a与32b等比中项,
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、4 | ||||
B、3+2
| ||||
C、
| ||||
| D、2 |
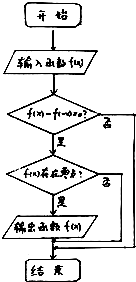 执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )
执行如图所示的程序框图,若输入如下四个函数①f(x)=sinx②f(x)=cosx③f(x)=e|x|④f(x)=|lnx|则输出的函数的个数为( )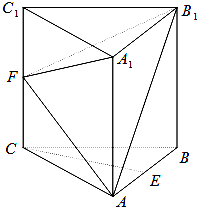 如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.
如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.