题目内容
给出下列命题:
①底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
②若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
③一个棱锥可以有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱一定是正方体.
其中正确的命题是( )
①底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
②若有两个侧面垂直于底面,则该四棱柱为直四棱柱;
③一个棱锥可以有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱一定是正方体.
其中正确的命题是( )
| A、①②③ | B、①③ | C、②③④ | D、④ |
考点:棱柱的结构特征,棱锥的结构特征
专题:空间位置关系与距离
分析:①底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥;
②当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱;
③一个棱锥不能有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱不一定是正方体.
②当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱;
③一个棱锥不能有两条侧棱和底面垂直;
④一个棱锥可以有两个侧面和底面垂直;
⑤所有侧面都是正方形的四棱柱不一定是正方体.
解答:
 解:对于①,底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,
解:对于①,底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,
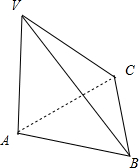
如图所示,
若AB=BC=AC=VA,且VA⊥平面ABC,但三棱锥V-ABC表示正三棱锥,∴①错误;
对于②,当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱,
如两个侧面不是相邻的时,侧棱与底面不一定垂直,∴②错误;
对于③,一个棱锥不能有两条侧棱和底面垂直,否则,这两条侧棱互相平行,∴③错误;
对于④,一个棱锥可以有两个侧面和底面垂直,如①中图形,∴④正确;
对于⑤,所有侧面都是正方形的四棱柱不一定是正方体,
∵各相邻侧面并不一定都互相垂直,∴⑤错误.
综上,正确的命题是④.
故选:D.
 解:对于①,底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,
解:对于①,底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,如图所示,
若AB=BC=AC=VA,且VA⊥平面ABC,但三棱锥V-ABC表示正三棱锥,∴①错误;
对于②,当有两个侧面垂直于底面时,该四棱柱不一定为直四棱柱,
如两个侧面不是相邻的时,侧棱与底面不一定垂直,∴②错误;
对于③,一个棱锥不能有两条侧棱和底面垂直,否则,这两条侧棱互相平行,∴③错误;
对于④,一个棱锥可以有两个侧面和底面垂直,如①中图形,∴④正确;
对于⑤,所有侧面都是正方形的四棱柱不一定是正方体,
∵各相邻侧面并不一定都互相垂直,∴⑤错误.
综上,正确的命题是④.
故选:D.
点评:本题考查了空间中的柱、锥、体的结构特征的应用问题,解题时应对每一个命题进行分析判断,是综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以双曲线y2-x2=2的一个焦点为圆心,离心率为半径的圆的方程是( )
| A、x2+(y±2)2=2 |
| B、(x±2)2+y2=2 |
| C、x2+(y±2)2=4 |
| D、(x±2)2+y2=4 |
一艘海轮从A处出发,以每小时60海里的速度沿东偏南50°方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是( )
A、10
| ||
B、10
| ||
C、15
| ||
D、20
|
 如图,在圆O中,已知弦AB=4,弦AC=6,那么
如图,在圆O中,已知弦AB=4,弦AC=6,那么| AO |
| BC |
| A、10 | ||
B、2
| ||
C、
| ||
| D、-10 |