Question

若实数x，y满足x²+y²-2x+4y=0，求（x+1）²+（y-1）²的最大值和最小值．

Answer 1

考点：直线和圆的方程的应用

专题：直线与圆

分析：（x+1）²+（y-1）²的几何意义为点（x，y）到定点（-1，1）的距离的平方，利用数形结合即可得到结论．

解答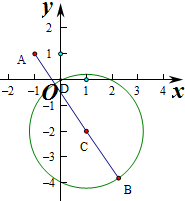： 解：x²+y²-2x+4y=0等价为（x-1）²+（y+2）²=5，圆心为C（1，-2），半径r=

5

，
设z=（x+1）²+（y-1）²，则z的几何意义为圆上点P（x，y）到定点A（-1，1）的距离的平方，
则|AC|=

(-1-1)2+(1+2)2

=

13

，则圆上点到A距离的最大值为

13

+

5

，最小值为

13

-

5

，
则z=（x+1）²+（y-1）²的最大值为（

13

+

5

）²和最小值（

13

-

5

）²．

点评：本题主要考查点到直线的距离公式的应用，直线和圆的位置关系，两点间的距离公式的应用，属于中档题，利用数形结合是解决本题的关键．．