题目内容
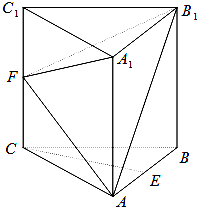 如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.
如图,在各棱长都相等的直三棱柱ABC-A1B1C1中,E,F分别为AB,CC1的中点.(Ⅰ)求证:CE∥平面AB1F;
(Ⅱ)求直线A1F与平面AB1F所成角的正弦值.
考点:直线与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(Ⅰ)利用三棱柱的性质连接A1B交AB1于D点,连接DE,DF得到四边形DECF为平行四边形,利用线面平行的判定定理可证;
(Ⅱ)∵直三棱柱ABC-A1B1C1各棱长都相等,E为AB的中点得到CE⊥A1B,由(Ⅰ) CE∥DF得DF⊥A1B,
所以A1D⊥平面AB1F,得到∠A1FD是A1F与平面AB1F所成的角,然后解Rt△A1DF即可.
(Ⅱ)∵直三棱柱ABC-A1B1C1各棱长都相等,E为AB的中点得到CE⊥A1B,由(Ⅰ) CE∥DF得DF⊥A1B,
所以A1D⊥平面AB1F,得到∠A1FD是A1F与平面AB1F所成的角,然后解Rt△A1DF即可.
解答:
 证明:(Ⅰ)如图示,连接A1B交AB1于D点,连接DE,DF
证明:(Ⅰ)如图示,连接A1B交AB1于D点,连接DE,DF
由题DE是△ABB1的中位线
∴DE∥BB1且DE=
BB1
即DE∥CF且DE=CF
∴四边形DECF为平行四边形
∴CE∥DF
又CE?平面AB1F,DF?平面AB1F
∴CE∥平面AB1F…6分
解:(Ⅱ)∵直三棱柱ABC-A1B1C1各棱长都相等,E为AB的中点
∴CE⊥AB,CE⊥AA1
∴CE⊥平面ABB1A1,又A1B?平面ABB1A1
∴CE⊥A1B
由(Ⅰ) CE∥DF得DF⊥A1B
又A1D⊥AB1,DF,AB1是平面AB1F内两条相交直线
∴A1D⊥平面AB1F
∴DF是A1F在平面AB1F上的射影
∴∠A1FD是A1F与平面AB1F所成的角 …9分
设直三棱柱ABC-A1B1C1的棱长为a
在Rt△A1DF中,AD=
a,AF=
=
a,
∴sin∠A_FD=
=
∴直线A1F与平面AB1F所成角的正弦值是
…12分.
 证明:(Ⅰ)如图示,连接A1B交AB1于D点,连接DE,DF
证明:(Ⅰ)如图示,连接A1B交AB1于D点,连接DE,DF由题DE是△ABB1的中位线
∴DE∥BB1且DE=
| 1 |
| 2 |
即DE∥CF且DE=CF
∴四边形DECF为平行四边形
∴CE∥DF
又CE?平面AB1F,DF?平面AB1F
∴CE∥平面AB1F…6分
解:(Ⅱ)∵直三棱柱ABC-A1B1C1各棱长都相等,E为AB的中点
∴CE⊥AB,CE⊥AA1
∴CE⊥平面ABB1A1,又A1B?平面ABB1A1
∴CE⊥A1B
由(Ⅰ) CE∥DF得DF⊥A1B
又A1D⊥AB1,DF,AB1是平面AB1F内两条相交直线
∴A1D⊥平面AB1F
∴DF是A1F在平面AB1F上的射影
∴∠A1FD是A1F与平面AB1F所成的角 …9分
设直三棱柱ABC-A1B1C1的棱长为a
在Rt△A1DF中,AD=
| ||
| 2 |
| AC2+CF2 |
| ||
| 2 |
∴sin∠A_FD=
| A_D |
| A_F |
| ||
| 5 |
∴直线A1F与平面AB1F所成角的正弦值是
| ||
| 5 |
点评:本题考查了三棱柱性质的运用以及线面平行的判定、线面角的求法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在圆O中,已知弦AB=4,弦AC=6,那么
如图,在圆O中,已知弦AB=4,弦AC=6,那么| AO |
| BC |
| A、10 | ||
B、2
| ||
C、
| ||
| D、-10 |
用秦九韶算法计算函数f(x)=3x4-2x3-6x-17,当x=2时,则f(x)的值为( )
| A、0 | B、2 | C、3 | D、-3 |
已知a,b为异面直线,则下列命题中正确的是( )
| A、过a,b外一点P一定可以引一条与a,b都平行的直线 |
| B、过a,b外一点P一定可以作一个与a,b都平行的平面 |
| C、过a一定可以作一个与b平行的平面 |
| D、过a一定可以作一个与b垂直的平面 |