题目内容
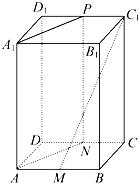如图，长方体ABCD-A1B1C1D1中，M，N，P分别为线段AB，CD，C1D1的中点．求证：（1）C1M∥平面ANPA1；
（2）平面C1MC∥平面ANPA1．
考点：直线与平面平行的判定,平面与平面平行的判定
专题：空间位置关系与距离
分析：（1）只要证明AP∥MC1，利用线面平行的判定定理；
（2）由（1）可得，C1M∥平面ANPA1，只要证明PN∥CC1，Z再由线面平行的判定定理证明．
（2）由（1）可得，C1M∥平面ANPA1，只要证明PN∥CC1，Z再由线面平行的判定定理证明．
解答：
证明：（1）因为长方体ABCD-A1B1C1D1中，M，N，P分别为线段AB，CD，C1D1的中点，
所以AM∥PC1，并且AM=PC1，
所以四边形AMC1P，是平行四边形，
所以AP∥MC1，
AP?平面ANPA1，MC1平面ANPA1
所以C1M∥平面ANPA1；
（2）由（1）C1M∥平面ANPA1，
长方体ABCD-A1B1C1D1中，N，P分别为线段CD，C1D1的中点，
所以PN∥CC1，
又因为MC1∩CC1=C1，AP∩PN=P，
所以平面C1MC∥平面ANPA1．
所以AM∥PC1，并且AM=PC1，
所以四边形AMC1P，是平行四边形，
所以AP∥MC1，
AP?平面ANPA1，MC1平面ANPA1
所以C1M∥平面ANPA1；
（2）由（1）C1M∥平面ANPA1，
长方体ABCD-A1B1C1D1中，N，P分别为线段CD，C1D1的中点，
所以PN∥CC1，
又因为MC1∩CC1=C1，AP∩PN=P，
所以平面C1MC∥平面ANPA1．
点评：本题长方体中线面平行和面面平行的判断；关键是将所证转化为线线关系，熟练面面平行的判定定理．
练习册系列答案
相关题目
若f（x）=
，则f（-2）=（ ）
|
| A、-2 | B、1 | C、2 | D、3 |
已知y=f（x）是偶函数，当x＞0时，f（x）=x+
，且x∈[-3，-1]时n≤f（x）≤m恒成立，则m-n的最小值是（ ）
| 4 |
| x |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
已知定点A（2014，2），F是抛物线y2=2x的焦点，点P是抛物线上的动点，当|PA|+|PF|最小时，点P的坐标为（ ）
| A、（0，0） | ||
B、（1，
| ||
| C、（2，2） | ||
D、（
|
