题目内容

若
e1
、
e2
是平面内的一组基底，则下列四组向量能作为平面向量的基底的是（　　）
A、
e1
-
e2
，
e2
-
e1
B、2
e1
-
e2
，
e1
-
1
2
e2
C、2
e2
-3
e1
，6
e1
-4
e2
D、
e1
+
e2
，
e1
-
e2
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：利用平面向量基本定理，作为平面向量基底的向量必须是不共线的向量，由此选择．
解答： 解：观察四个选项，对于选项A，
e1
-
e2
=-(
e2
-
e1
)；
B，2
e1
-
.
e2
=2(
e1
-
1
2
e2
)，
C，-2(2
e2
-3
e1
)=6
e1
-4
e2
，
两个向量都是共线向量，所以不能作为基底，
故选D．
点评：本题考查了平面向量基本定理的运用；注意能作为基底的平面向量必须是不共线的向量．
练习册系列答案
相关题目
函数f（x）=
x2+1
+
x2-6x+10
的性质：
①f（x）的图象是中心对称图形；
②f（x）的图象是轴对称图形；
③函数f（x）的值域为[
13
，+∞）；
④方程f（f（x））=1+
10
有两个解，上述关于函数的性质说法正确的是（　　）
A、①③B、③④C、②③D、②④
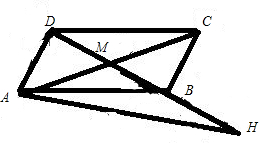如图，平行四边形ABCD的两条对角线相交于点M，
AB
=
a
，
AD
=
b
，在DB延长线上取点H，使BH=MB，若
AH
=λ1
a
+λ2
b
，则λ1=
 
，λ2=
 
．
设f（x）=sin2x-2acosx+1，最大值记为g（a），求g（a）的表达式及值域．
已知函数f（x）=2sin（2x+
π
6
）+a+1，且当x∈[0，
π
6
]时，f（x）的最小值为2．
（1）求的a值，并求f（x）单调递增区间；
（2）将函数f（x）图象上各点的纵坐标保持不变，横坐标缩短到原来的
1
2
倍，再把所得图象向右平移
π
12
个单位，得到函数g（x），求方程g（x）=2在区间[0，
π
2
]上的所有根之和．
一家化妆品公司在今年三八节期间开了“洗发水，洗面奶，护肤霜”三场讲座，甲、乙两人去参加者三场讲座中的一场，且每人参加每场讲座的可能性相同，求：
（1）甲、乙参加同一场讲座的概率；
（2）甲、乙都没有参加“洗发水”讲座的概率．
若f（x）=
lgx，x＞0
f(x+1)+1，x≤0
，则f（-2）=（　　）
A、-2B、1C、2D、3
阅读如图所示的程序框图，运行相应的程序，则输出的结果是
 
．
设椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0），离心率e=
2
2
，O为原点坐标原点，且椭圆的一短轴端点到一焦点的距离为4
2
．
（1）求椭圆E的方程
（2）若M（X0，Y0）为椭圆E上的动点，其中2＜Y0＜
31
2
，过点M作圆x2+（y-1）2=1的两切线，两切线与x轴围成的三角形面积为S，求S关于y0的函数解析式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网