题目内容

设A={x|-2＜x≤2}，B={x|0≤x≤4}，求A∩B．
考点：交集及其运算
专题：集合
分析：直接利用交集的运算法则求出A∩B即可．
解答： 解：∵A={x|-2＜x≤2}，B={x|0≤x≤4}，
∴A∩B={x|0≤x≤2}
点评：本题考查交集的基本运算，注意两个集合的相同元素组成的集合是两个集合的交集．
练习册系列答案
相关题目
已知数列{an}满足Sn=
n(a1+an)
2
，其中Sn是数列{an}的前n项和．
（1）证明：数列{an}是等差数列；
（2）若a1=1，S2=4，求数列{
an
2n-1
}的最大值项．
已知M是所有同时满足下列性质的函数f（x）的集合：
①函数f（x）在其定义域是单调函数；
②在函数f（x）的定义域内存在区间[a，b]，使得f（x）在[a，b]上的最小值是a，最大值是b．
（1）判断函数f（x）=x2，x∈[0，+∞）是否属于集合M？若是，请求出相应的区间[a，b]；若不是，请说明理由；
（2）证明：函数f（x）=3log2x属于集合M；
（3）若函数f（x）=
mx
1+|x|
属于M，求实数m的取值范围．
函数f（x）=
x2+1
+
x2-6x+10
的性质：
①f（x）的图象是中心对称图形；
②f（x）的图象是轴对称图形；
③函数f（x）的值域为[
13
，+∞）；
④方程f（f（x））=1+
10
有两个解，上述关于函数的性质说法正确的是（　　）
A、①③B、③④C、②③D、②④
设a＜-1，则关于x的不等式a（x-a）（x-
1
a
）＜0的解集是（　　）
A、{x|x＜a或＞
1
a
}
B、{x|x＞a}
C、{x|x＞a或x＜
1
a
}
D、{x|x＜
1
a
}
若
e
是
b
的单位向量，
a
与
e
的方向相反，且|
b
|=3，|
a
|=4，则
a
=
 
b
．
函数f（x）=|4sin（2x+（
π
6
））|的最小正周期为（　　）
A、
π
4
B、
π
2
C、π
D、2π
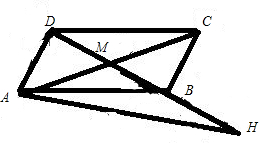如图，平行四边形ABCD的两条对角线相交于点M，
AB
=
a
，
AD
=
b
，在DB延长线上取点H，使BH=MB，若
AH
=λ1
a
+λ2
b
，则λ1=
 
，λ2=
 
．
若f（x）=
lgx，x＞0
f(x+1)+1，x≤0
，则f（-2）=（　　）
A、-2B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网