题目内容
证明f（x）=-x2在（-∞，0）上是增函数，在（0，+∞）上是减函数．
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：利用定义证明函数的单调性．
解答：
证明：设任意的x1，x2∈（-∞，0），且x1＜x2，则
f（x1）-f（x2）=-
-（-
）=（x2-x1）（x2+x1）
∵x1，x2∈（-∞，0），且x1＜x2，
∴x2-x1＞0，x2+x1＜0，
∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴函数f（x）=-x2在（-∞，0）上是增函数．
同理可证函数f（x）=-x2在（0，+∞）上是减函数．
f（x1）-f（x2）=-
| x | 2 1 |
| x | 2 2 |
∵x1，x2∈（-∞，0），且x1＜x2，
∴x2-x1＞0，x2+x1＜0，
∴f（x1）-f（x2）＜0，即f（x1）＜f（x2），
∴函数f（x）=-x2在（-∞，0）上是增函数．
同理可证函数f（x）=-x2在（0，+∞）上是减函数．
点评：本题主要考查利用函数的单调性定义证明函数单调性的方法，关键在于判断差的符号，属基础题．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
下列命题中的真命题是（ ）
| A、?x∈R，x2＞0 | ||
B、?x∈R，x+
| ||
| C、?x0∈R，sinx0+cosx0=2 | ||
D、?x0∈R，ln x0＞（
|
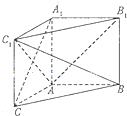如图，在直三棱柱ABC-A1B1C1中，AB⊥AC，且AB=AC=AA1=1．