题目内容
4.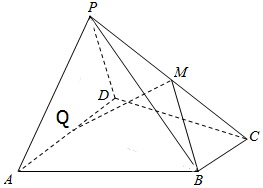 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4(1)求证:直线PA∥平面QMB;
(2)若PC=2$\sqrt{5}$,求三棱锥P-MBQ的体积.
分析 (1)连结BQ,AC,交于点O,推导出四边形BCDQ是矩形,从而BQ∥CD,再求出OM∥PA,由此能证明直线PA∥平面QMB.
(2)由点P到平面BQM的距离等于点A到平面BMQ的距离,从而VP-MBQ=VA-MBQ=VM-ABQ,由此能求出三棱锥P-MBQ的体积.
解答 证明:(1)连结BQ,AC,交于点O,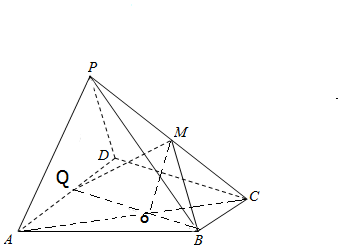
∵Q是AD中点,∴BC∥QD,BC=QD,
∴四边形BCDQ是矩形,
∴BQ∥CD,又Q是AD中点,
∴O是AC中点,又M是PC的中点,
∴OM∥PA,又OM?面QMB,PA?平面QMB,
∴直线PA∥平面QMB.
解:(2)由(1)知PA∥平面QBM,
∴点P到平面BQM的距离等于点A到平面BMQ的距离,
∴VP-MBQ=VA-MBQ=VM-ABQ,
∵PA=PC=PD=2$\sqrt{5}$,
∴点P在平面ADC内的射影是△ADC的外心,
又△ADC是直角三角形,
∴点P在平面ABC内的射影是AC的中点O,即PO⊥平面ABCD,
在Rt△PAO中,
∵PA=2$\sqrt{5}$,AO=$\frac{1}{2}$AC=$\frac{1}{2}$$\sqrt{A{D}^{2}+C{D}^{2}}$=$\frac{1}{2}\sqrt{{4}^{2}+{4}^{2}}$=2$\sqrt{2}$,
∴PO=$\sqrt{P{A}^{2}-A{O}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{3}$,
∵M是PC的中点,
∴点M到平面ABQ的距离等于$\frac{1}{2}$PO=$\sqrt{3}$,
∴三棱锥P-MBQ的体积VP-MBQ=VM-ABQ=$\frac{1}{3}{S}_{△ABQ}•h$=$\frac{1}{3}×\frac{1}{2}×2×4×\sqrt{3}$=$\frac{4\sqrt{3}}{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | 2 | B. | $4\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 8 |
| A. | 若 $α≠\frac{π}{4}$,则tanα≠1 | B. | 若 $α=\frac{π}{4}$,则tanα≠1 | ||
| C. | 若 tanα≠1,则$α≠\frac{π}{4}$ | D. | 若 tanα≠1,则$α=\frac{π}{4}$ |
| A. | $y=3sin(2x-\frac{π}{6})$ | B. | y=3cos2x | C. | $y=3sin(2x+\frac{π}{3})$ | D. | y=3sin2x |
| A. | {x|-l≤x≤2} | B. | {x|-1<x<2} | C. | {x|x≥2,或-1≤-1} | D. | {x|x>2,或x<-1} |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |