双曲线$\frac{x^2}{16}-\frac{y^2}{8}=1$的虚轴长是( )A．2B．$4\sqrt{2}$C．$2\sqrt{2}$D．8 题目和参考答案——青夏教育精英家教网—

题目内容

14．双曲线$\frac{x^2}{16}-\frac{y^2}{8}=1$的虚轴长是（　　）

A．

B．

$4\sqrt{2}$

C．

$2\sqrt{2}$

D．

分析根据题意，由双曲线的标准方程可得b的值，进而由虚轴长为2b，计算可得答案．

解答解：根据题意，双曲线的标准方程为$\frac{x^2}{16}-\frac{y^2}{8}=1$，
则其中b=$\sqrt{8}$=2$\sqrt{2}$，
则虚轴的长2b=4$\sqrt{2}$；
故选：B．

点评本题考查双曲线的标准方程，注意虚轴的长是2b．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

5．已知二次函数f（x）=x²-ax+a（x∈R）同时满足：
①不等式f（x）≤0的解集有且只有一个元素；
②在定义域内存在0＜x₁＜x₂，使得不等式f（x₁）＞f（x₂）成立．
设数列{a_n}的前n项和S_n=f（n）．
（1）求函数f（x）的表达式；
（2）设各项均不为0的数列{b_n}中，所有满足b_i•b_i+1＜0的整数i的个数称为这个数列{b_n}的变号数，令${b_n}=1-\frac{a}{a_n}$（n∈N^*），求数列{b_n}的变号数；
（3）设数列{c_n}满足：${c_n}=\sum_{i=1}^n{\frac{1}{{{a_i}•{a_{i+1}}}}}$，试探究数列{c_n}是否存在最小项？若存在，求出该项，若不存在，说明理由．

2．已知集合A={x||x|＜1}，B={x|x²-x＜0}，则A∩B=（　　）

9．已知△ABC的三顶点分别为A（1，4，1），B（1，2，3），C（2，3，1）．则AB边上的高等于（　　）

A．

$\frac{{\sqrt{6}}}{2}$

19．已知定点M（-3，0），N（2，0），如果动点P满足|PM|=2|PN|，则点P的轨迹所包围的图形面积等于（　　）

6．若f（x）是定义域为R，最小正周期$\frac{3π}{2}$的函数，若f（x）=sinx，x∈[0，π]，则f（$\frac{15π}{4}$）=$\frac{\sqrt{2}}{2}$．

3．已知集合A={x|2≤2^x≤8}，B={x|x＞2}，全集U=R．
（1）求（∁_UB）∪A；
（2）已知集合C={x|1＜x＜a}，若C⊆A，求实数a的取值范围．

4．

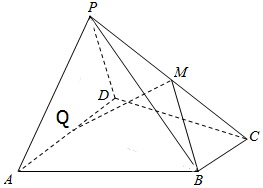如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，Q为AD的中点，M是棱PC的中点，PA=PD=PC，BC=$\frac{1}{2}$AD=2，CD=4
（1）求证：直线PA∥平面QMB；
（2）若PC=2$\sqrt{5}$，求三棱锥P-MBQ的体积．

试题分类