题目内容
19.(1)已知a为常数,且0<a<1,函数f(x)=(1+x)a-ax,求函数f(x)在x>-1上的最大值;(2)若a,b均为正实数,求证:ab+ba>1.
分析 (1)由f′(x)=a(1+x)a-1-a=a[(1+x)a-1-1],当-1<x<0时,f′(x)>0,当x>0,f′(x)<0,f(x)在x=0处取极大值,也是最大值f(0)=1;
(2)①当a,b中有一个大于1时,不妨设a≥1,ab+ba>ab>1,②当a,b均属于(0,1),设a=$\frac{1}{1+m}$,b=$\frac{1}{1+n}$,(m,n>0),则ab=$(\frac{1}{1+m})^{\frac{1}{1+n}}$=$\frac{1}{(1+m)^{\frac{1}{1+n}}}$≥$\frac{1}{1+\frac{m}{1+n}}$=$\frac{1+n}{1+m+n}$,同理ba≥$\frac{1+m}{1+m+n}$,即可证明ab+ba>1.
解答 解:(1)由f(x)=(1+x)a-ax,求导f′(x)=a(1+x)a-1-a=a[(1+x)a-1-1],
当-1<x<0时,f′(x)>0,当x>0,f′(x)<0,
∴f(x)在x=0处取极大值,也是最大值f(0)=1,
∴f(x)的最大值为1;
(2)证明:①当a,b中有一个大于1时,不妨设a≥1,
ab+ba>ab>1,
②当a,b均属于(0,1),设a=$\frac{1}{1+m}$,b=$\frac{1}{1+n}$,(m,n>0),
则ab=$(\frac{1}{1+m})^{\frac{1}{1+n}}$=$\frac{1}{(1+m)^{\frac{1}{1+n}}}$≥$\frac{1}{1+\frac{m}{1+n}}$=$\frac{1+n}{1+m+n}$,
同理可知:ba≥$\frac{1+m}{1+m+n}$,
∴ab+ba>$\frac{1+n}{1+m+n}$+$\frac{1+m}{1+m+n}$=$\frac{2+m+n}{1+m+n}$>1,
∴ab+ba>1.
点评 本题考查利用导数求函数的单调性及极值,考查不等式的证明,考查分类讨论思想,属于中档题.

| A. | (2x+2)5 | B. | 2x5 | C. | (2x-1)5 | D. | 32x5 |
①|$\sqrt{(x+4)^{2}+{y}^{2}}$|-|$\sqrt{(x-4)^{2}+{y}^{2}}$=0
②|$\sqrt{(x+4)^{2}+{y}^{2}}$+$\sqrt{(x-4)^{2}+{y}^{2}}$=14
③|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=6
④|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=18.
| A. | ①表示无轨迹 ②的轨迹是射线 | B. | ②的轨迹是椭圆 ③的轨迹是双曲线 | ||
| C. | ①的轨迹是射线④的轨迹是直线 | D. | ②、④均表示无轨迹 |
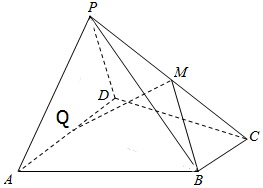 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4