题目内容
2.已知函数f(x)=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x+1)^{2}+1}$,则f(x)的最小值为2$\sqrt{2}$.分析 由f(x)=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x+1)^{2}+1}$的几何意义:点(x,0)到(1,1)与(-1,1)的距离之和,过B作x轴的对称点D(1,-1),当C与O点重合时,丨AC丨+丨BC丨,取最小值,f(x)min=丨AD丨=$\sqrt{[1-(-1)]^{2}+(-1-1)^{2}}$=2$\sqrt{2}$.
解答 解:由f(x)=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x+1)^{2}+1}$的几何意义:点(x,0)到(1,1)与(-1,1)的距离之和,
即f(x)表示丨AC丨+丨BC丨,
过B作x轴的对称点D(1,-1),
连接AD,交x轴于O点,
∴当C与O点重合时,丨AC丨+丨BC丨,取最小值,
∴f(x)min=丨AD丨=$\sqrt{[1-(-1)]^{2}+(-1-1)^{2}}$=2$\sqrt{2}$,
函数f(x)=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x+1)^{2}+1}$的最小值为:2$\sqrt{2}$,
故答案为:2$\sqrt{2}$. \
\
点评 本题考查点到直线的距离公式的几何意义,考查数形结合思想,函数的最值,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.若某程序框图如图所示,则该程序运行后输出的B等于( )


| A. | 2 | B. | 5 | C. | 14 | D. | 41 |
11.设双曲线C:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的上、下焦点分别为F1,F2,若在双曲线C的下支上存在一点P使得|PF1|=4|PF2|,则双曲线C的离心率的取值范围为( )
| A. | [$\frac{4}{3}$,+∞) | B. | (1,$\frac{4}{3}$] | C. | [$\frac{5}{3}$,+∞) | D. | (1,$\frac{5}{3}$] |
14.化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是( )
| A. | (2x+2)5 | B. | 2x5 | C. | (2x-1)5 | D. | 32x5 |
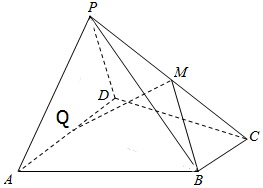 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,Q为AD的中点,M是棱PC的中点,PA=PD=PC,BC=$\frac{1}{2}$AD=2,CD=4