Question

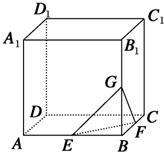如图，在棱长为4的正方体ABCD-A₁B₁C₁D₁中，点E、F、G分别为AB、BC、BB₁的中点．则以B为顶点的三棱锥B-GEF的高h=

 

．

Answer 1

考点：棱锥的结构特征

专题：计算题,空间位置关系与距离

分析：变换三棱锥的顶点，求出体积，由体积确定三棱锥的高．

解答： 解：∵S_△BEF=

1

2

BE•BF=

1

2

×2×2=2，BG=2，
∴三棱锥G-BEF的体积=V=

1

3

×2×2=

4

3

；
若以B为顶点，则底面为正三角形GEF，
其边长为EF=

BE2+BF2

=2

2

，
∴S_△GEF=

3

4

×（2

2

）²=2

3

．
又∵三棱锥B-GEF和三棱锥G-BEF的体积相等，
∴当以B为顶点时，三棱锥的高h=

4 3 ×3

2 3

=

2 3

3

．
故答案为

2 3

3

．

点评：本题考查了学生的空间想象力及体积的计算，属于基础题．