题目内容
已知函数f(x)=xn-
,且f(4)=3.
(1)求n的值,并判断该函数的奇偶性;
(2)若不等式f(x)-a>0在[1,+∞)上恒成立,求实数a的取值范围.
| 4 |
| x |
(1)求n的值,并判断该函数的奇偶性;
(2)若不等式f(x)-a>0在[1,+∞)上恒成立,求实数a的取值范围.
考点:函数恒成立问题,函数奇偶性的判断
专题:函数思想,函数的性质及应用
分析:(1)利用函数的奇偶性的概念判断,
(2)把不等式的恒成立问题转化为求函f(x)的最值问题解决,而求最值时利用函数的单调性.
(2)把不等式的恒成立问题转化为求函f(x)的最值问题解决,而求最值时利用函数的单调性.
解答:
解:(1)∵f(4)=3,
∴4n-
=3,则n=1.f(x)=x-
.函数的定义域为 (-∞,0)∪(0,+∞),
又∵f(-x)=-x-
=-(x-
)=-f(x),
∴函数f(x)=x-
是奇函数,
(2)∵函数y=x和y=-
在[1,+∞)上都是增函数,
∴函数f(x)=x-
在[1,+∞)上是增函数,
∴f(x)≥f(1)=-3.
不等式f(x)-a>0在[1,+∞)上恒成立,即不等式a<f(x)在[1,+∞)上恒成立.
∴a<-3,
即a的取值范围是(-∞,-3).
∴4n-
| 4 |
| 4 |
| 4 |
| x |
又∵f(-x)=-x-
| 4 |
| -x |
| 4 |
| x |
∴函数f(x)=x-
| 4 |
| x |
(2)∵函数y=x和y=-
| 1 |
| x |
∴函数f(x)=x-
| 4 |
| x |
∴f(x)≥f(1)=-3.
不等式f(x)-a>0在[1,+∞)上恒成立,即不等式a<f(x)在[1,+∞)上恒成立.
∴a<-3,
即a的取值范围是(-∞,-3).
点评:本题考查了函数的奇偶性概念,含有参变量的不等式恒成立问题,构造函数求最值来解决,思路很容易想.

练习册系列答案
相关题目
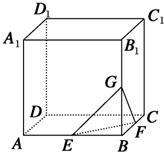 如图,在棱长为4的正方体ABCD-A1B1C1D1中,点E、F、G分别为AB、BC、BB1的中点.则以B为顶点的三棱锥B-GEF的高h=
如图,在棱长为4的正方体ABCD-A1B1C1D1中,点E、F、G分别为AB、BC、BB1的中点.则以B为顶点的三棱锥B-GEF的高h= 如图,已知在200m高的山顶A处,测得山下一塔顶B与塔底C的俯角分别是30°,
如图,已知在200m高的山顶A处,测得山下一塔顶B与塔底C的俯角分别是30°,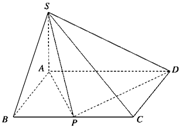 如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,SA=AB=1.则PD与平面SAP所成的角的大小为
如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,SA=AB=1.则PD与平面SAP所成的角的大小为