题目内容
已知定义域R的函数f(x)为偶函数,且f(x+2)=f(x)对任意实数x恒成立,当0≤x≤1时,f(x)=x.
(1)求当-1≤x<0时,f(x)的解析式;
(2)求当x∈[2k-1,2k+1),(k∈Z)时,函数f(x)的解析式;
(3)求方程f(x)=
在区间[-1,2013]内的所有解的集合.
(1)求当-1≤x<0时,f(x)的解析式;
(2)求当x∈[2k-1,2k+1),(k∈Z)时,函数f(x)的解析式;
(3)求方程f(x)=
| 1 |
| 2 |
考点:根的存在性及根的个数判断,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)当-1≤x<0时,0≤-x<1,从而f(x)=f(-x)=-x;
(2)由(1)及已知得当x∈[2k-1,2k+1),(k∈Z)时,从而f(x)=|x-2k|;
(3)f(x)=
?|x-2k|=
?x=2k±
,k∈Z,求出k的范围即可.
(2)由(1)及已知得当x∈[2k-1,2k+1),(k∈Z)时,从而f(x)=|x-2k|;
(3)f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)当-1≤x<0时,0≤-x<1,
∴f(-x)=-x,
∴f(x)=f(-x)=-x,
故当-1≤x<0时,
∴f(x)=-x;
(2)由(1)及已知得
当-1≤x<1时f(x)=|x|,
当x∈[2k-1,2k+1),(k∈Z)时,
x-2k∈[-1,1),
∴f(x-2k)=|x-2k|,
又f(x+2)=f(x),
∴f(x-2k)=f(x),
所以f(x)=|x-2k|.
故f(x)=|x-2k|,x∈[2k-1,2k+1),(k∈Z),
(3)f(x)=
?|x-2k|=
?x=2k±
,k∈Z,
故f(x)=y在[-1,2013]内的解集为{x|x=2k±
,k∈Z,k=0,1,2,…,1006}.
∴f(-x)=-x,
∴f(x)=f(-x)=-x,
故当-1≤x<0时,
∴f(x)=-x;
(2)由(1)及已知得
当-1≤x<1时f(x)=|x|,
当x∈[2k-1,2k+1),(k∈Z)时,
x-2k∈[-1,1),
∴f(x-2k)=|x-2k|,
又f(x+2)=f(x),
∴f(x-2k)=f(x),
所以f(x)=|x-2k|.
故f(x)=|x-2k|,x∈[2k-1,2k+1),(k∈Z),
(3)f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故f(x)=y在[-1,2013]内的解集为{x|x=2k±
| 1 |
| 2 |
点评:本题考查了根的存在性,考查函数解析式的求法,本题属于中档题.

练习册系列答案
相关题目
方程x3-(
)x-2=0的根所在的区间为( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
 某校为了解学生的体重发育情况,现从600名高一男生体检评价报告单中随机抽出50名学生的体重(单位:kg)数据进行整理后分成五组,得到频率分布表如下:
某校为了解学生的体重发育情况,现从600名高一男生体检评价报告单中随机抽出50名学生的体重(单位:kg)数据进行整理后分成五组,得到频率分布表如下: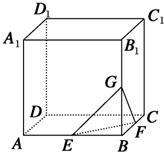 如图,在棱长为4的正方体ABCD-A1B1C1D1中,点E、F、G分别为AB、BC、BB1的中点.则以B为顶点的三棱锥B-GEF的高h=
如图,在棱长为4的正方体ABCD-A1B1C1D1中,点E、F、G分别为AB、BC、BB1的中点.则以B为顶点的三棱锥B-GEF的高h=