题目内容
平面内动点M到点F（1，0）的距离比它到y轴的距离大1，动点M的轨迹记为曲线C．
（1）求曲线C的方程；
（2）A，B是曲线C上的两点，O是原点，若△OAB是等边三角形，求OA的长．
（1）求曲线C的方程；
（2）A，B是曲线C上的两点，O是原点，若△OAB是等边三角形，求OA的长．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：（1）设动点M的坐标为（x，y），根据动点M到点F（1，0）的距离比它到y轴的距离大1，建立方程，化简可得点M的轨迹C的方程；
（2）由对称性，设A（
，y），则tan30°=
=
，即可求OA的长．
（2）由对称性，设A（
| y2 |
| 4 |
| y | ||
|
| 4 |
| y |
解答：
解：（1）设动点M的坐标为（x，y），
由题意，∵动点M到点F（1，0）的距离比它到y轴的距离大1，
∴
=|x|+1；
化简得y2=4x或y=0（x≤0），
所以点M的轨迹C的方程为y2=4x或y=0（x≤0）；
（2）由对称性，设A（
，y），则tan30°=
=
，
∴y=4
，
∴|OA|=2y=8
．
由题意，∵动点M到点F（1，0）的距离比它到y轴的距离大1，
∴
| (x-1)2+y2 |
化简得y2=4x或y=0（x≤0），
所以点M的轨迹C的方程为y2=4x或y=0（x≤0）；
（2）由对称性，设A（
| y2 |
| 4 |
| y | ||
|
| 4 |
| y |
∴y=4
| 3 |
∴|OA|=2y=8
| 3 |
点评：本题考查轨迹方程，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
如图已知正方体ABCD-A1B1C1D1的棱长为3，点M在AC上，点N在BC1上，且|AM|=2|MC|，|BN|=2|NC|．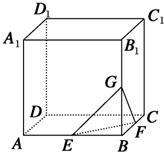
如图，在棱长为4的正方体ABCD-A1B1C1D1中，点E、F、G分别为AB、BC、BB1的中点．则以B为顶点的三棱锥B-GEF的高h=