题目内容
解不等式:
(Ⅰ)|1-2x|≤3;
(Ⅱ)1≤|x+1|<5.
(Ⅰ)|1-2x|≤3;
(Ⅱ)1≤|x+1|<5.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(I)原不等式化为|2x-1|≤3,得-3≤2x-1≤3,从而求得不等式的解集.
(II)原不等式同解于
,即
,由此求得不等式的解集.
(II)原不等式同解于
|
|
解答:
解:(I)原不等式化为|2x-1|≤3,得-3≤2x-1≤3,从而-2≤2x≤4,得解集为{x|-1≤x≤2}.
(II)原不等式同解于
,即
,
原不等式化为
,故不等式的解集为(-6,-2]∪[0,4).
(II)原不等式同解于
|
|
原不等式化为
|
点评:本题主要考查绝对值不等式的解法,体现了等价转化的数学思想,属于基础题.

练习册系列答案
相关题目
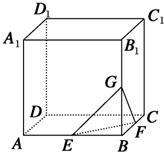 如图,在棱长为4的正方体ABCD-A1B1C1D1中,点E、F、G分别为AB、BC、BB1的中点.则以B为顶点的三棱锥B-GEF的高h=
如图,在棱长为4的正方体ABCD-A1B1C1D1中,点E、F、G分别为AB、BC、BB1的中点.则以B为顶点的三棱锥B-GEF的高h= 如图,已知在200m高的山顶A处,测得山下一塔顶B与塔底C的俯角分别是30°,
如图,已知在200m高的山顶A处,测得山下一塔顶B与塔底C的俯角分别是30°,