题目内容
（文）已知3sinx-cosx=0则则
= ．
| sin2x-sin2x |
| cos2x |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：由已知等式变形，求出tanx的值，原式分子分母除以cos2x后，将tanx的值代入计算即可求出值．
解答：
解：∵3sinx-cosx=0，∴tanx=
，
则原式=
=
=tan2x-2tanx=
-
=-
．
故答案为：-
| 1 |
| 3 |
则原式=
| sin2x-2sinxcosx |
| cos2x |
| tan2x-2tanx |
| 1 |
| 1 |
| 9 |
| 2 |
| 3 |
| 5 |
| 9 |
故答案为：-
| 5 |
| 9 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
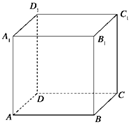如图已知正方体ABCD-A1B1C1D1的棱长为3，点M在AC上，点N在BC1上，且|AM|=2|MC|，|BN|=2|NC|．
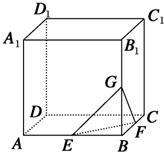如图，在棱长为4的正方体ABCD-A1B1C1D1中，点E、F、G分别为AB、BC、BB1的中点．则以B为顶点的三棱锥B-GEF的高h=
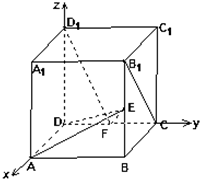在正方体ABCD-A1B1C1D1中，如图E、F分别是BB1，CD的中点，