题目内容
设两个非零向量
和
不共线．
（1）如果
=
+
，
=2
+8
，
=3
-3
，求证：A、B、D三点共线；
（2）若|
|=2，|
|=3，
与
的夹角为60°，是否存在实数m，使得m
+
与
-
垂直？并说明理由．
| e1 |
| e2 |
（1）如果
| AB |
| e1 |
| e2 |
| BC |
| e1 |
| e2 |
| CD |
| e1 |
| e2 |
（2）若|
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）首先利用向量的加法运算，得到
，然后观察与
的共线关系判断三点共线；
（2）假设存在m，利用向量垂直，数量积为0，得到m的方程，解方程即可．
| AD |
| AB |
（2）假设存在m，利用向量垂直，数量积为0，得到m的方程，解方程即可．
解答：
证明：（1）∵
=
+
+
=（
+
）+（2
+8
）+（3
-3
）
=6（
+
）=6
（3分）
∴
∥
且
与
有共同起点（5分）
∴A、B、D三点共线（6分）
（2）假设存在实数m，使得m
+
与
-
垂直，
则（m
+
）•（
-
）=0
∴m
2+(1-m)
•
-
2=0（8分）
∵|
|=2，|
|=3，
与
的夹角为60°
∴
2=|
|2=4，
2=|
|2=9，
•
=|
||
|cosθ=2×3×cos60°=3
∴4m+3（1-m）-9=0
∴m=6
故存在实数m=6，使得m
+
与
-
垂直．（12分）
| AD |
| AB |
| BC |
| CD |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
=6（
| e1 |
| e2 |
| AB |
∴
| AD |
| AB |
| AD |
| AB |
∴A、B、D三点共线（6分）
（2）假设存在实数m，使得m
| e1 |
| e2 |
| e1 |
| e2 |
则（m
| e1 |
| e2 |
| e1 |
| e2 |
∴m
| e1 |
| e1 |
| e2 |
| e2 |
∵|
| e1 |
| e2 |
| e1 |
| e2 |
∴
| e1 |
| e1 |
| e2 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
∴4m+3（1-m）-9=0
∴m=6
故存在实数m=6，使得m
| e1 |
| e2 |
| e1 |
| e2 |
点评：本题考查了利用向量共线判断三点共线以及向量垂直的性质．
练习册系列答案
相关题目
某校为了解学生的体重发育情况，现从600名高一男生体检评价报告单中随机抽出50名学生的体重（单位：kg）数据进行整理后分成五组，得到频率分布表如下：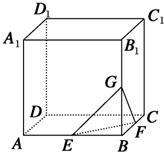
如图，在棱长为4的正方体ABCD-A1B1C1D1中，点E、F、G分别为AB、BC、BB1的中点．则以B为顶点的三棱锥B-GEF的高h=
如图，已知在200m高的山顶A处，测得山下一塔顶B与塔底C的俯角分别是30°，