题目内容
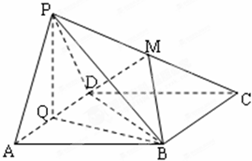 如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.(1)求证:PA∥平面MBD;
(2)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)连结AC交BD于O点,连结OM,可得OM是△PAC的中位线,可得PA∥OM,利用线面平行判定定理,即可证出PA∥平面MBD;
(2)正△PAD中,Q为AD的中点,故PQ⊥AD,利用面面垂直的性质定理,证出等边△PAD的高PQ⊥底面ABCD,从而得出CN⊥PQ,根据线面垂直的判定证出CN⊥平面PQB,从而得到平面PCN⊥平面PQB.由此可得在线段AB上存在AB的中点N,使得平面PCN⊥平面PQB.
(2)正△PAD中,Q为AD的中点,故PQ⊥AD,利用面面垂直的性质定理,证出等边△PAD的高PQ⊥底面ABCD,从而得出CN⊥PQ,根据线面垂直的判定证出CN⊥平面PQB,从而得到平面PCN⊥平面PQB.由此可得在线段AB上存在AB的中点N,使得平面PCN⊥平面PQB.
解答:
解:(1)连AC交BD于O,连MO则O为AC中点,因为M为PC中点,
所以MO∥AP,又AP?平面MBD,MO?平面MBD,则AP∥平面MBD.
(2)当BN=
时,平面PCN⊥平面PQB.
证明如下:正△PAD中,Q为AD的中点,故PQ⊥AD
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PQ⊥底面ABCD,
又CN?平面ABCD,则PQ⊥CN
又因为长方形ABCD中,由相似三角形得,则CN⊥BQ,
∴CN⊥平面PQB,
又∵CN?平面PCN,
所以,平面PCN⊥平面PQB.
所以MO∥AP,又AP?平面MBD,MO?平面MBD,则AP∥平面MBD.

(2)当BN=
| 1 |
| 2 |
证明如下:正△PAD中,Q为AD的中点,故PQ⊥AD
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PQ⊥底面ABCD,
又CN?平面ABCD,则PQ⊥CN
又因为长方形ABCD中,由相似三角形得,则CN⊥BQ,
∴CN⊥平面PQB,
又∵CN?平面PCN,
所以,平面PCN⊥平面PQB.
点评:本题在四棱锥中证明线面平行、并探索面面垂直的存在性.着重考查了线面垂直的判定与性质、面面垂直的判定与性质和线面平行判定定理等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在刚刚结束的校运会中,学校要求高一年级全体在篮球场观看比赛,如图所示,某同学为了拍摄下本班同学100m短跑的全过程,希望拍摄点P与100米的起点A,终点B的张角最大,现做如下数学模型:记百米跑道为4个单位(每单位25米),终点B离观赛区直线l距离为1单位,每个班的间距为1单位,如图所示,问该同学最好到哪个班所在的区域拍摄( )
在刚刚结束的校运会中,学校要求高一年级全体在篮球场观看比赛,如图所示,某同学为了拍摄下本班同学100m短跑的全过程,希望拍摄点P与100米的起点A,终点B的张角最大,现做如下数学模型:记百米跑道为4个单位(每单位25米),终点B离观赛区直线l距离为1单位,每个班的间距为1单位,如图所示,问该同学最好到哪个班所在的区域拍摄( )| A、12班 | B、11班 |
| C、10班 | D、9班 |
点P在直线x+y-4=0上,O为原点,则|OP|的最小值是( )
| A、2 | ||
B、
| ||
C、2
| ||
D、
|
已知△ABC的内角A,B,C所对应的边分别为a,b,c,若cosC>
,则△ABC的形状是( )
| b |
| a |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、钝角三角形 |