题目内容
已知点A的坐标为(1,0),点P(x,y)(x≠1)为圆(x-2)2+y2=1上的任意一点,设直线AP的倾斜角为θ,若|AP|=d,则函数d=f(θ)的大致图象是( )
A、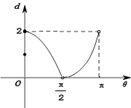 |
B、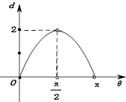 |
C、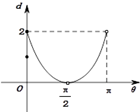 |
D、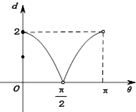 |
考点:函数的图象
专题:
分析:分两种情况考虑,当直线OP过第一象限与当直线OP过第四象限,画出函数图象,即可得到结果.
解答:
解:当直线OP过第一象限时,如图:

由于AB为直径,故θ=∠PAB=
,
得到d=f(θ)=2cosθ(0≤θ<
),
当直线OP过第四象限时,同理可得到d=f(π-θ)=2cos(π-θ)=-2cosθ(
<θ≤π),
函数d=f(θ)的大致图象:

故选:D.

由于AB为直径,故θ=∠PAB=
| π |
| 2 |
得到d=f(θ)=2cosθ(0≤θ<
| π |
| 2 |
当直线OP过第四象限时,同理可得到d=f(π-θ)=2cos(π-θ)=-2cosθ(
| π |
| 2 |
函数d=f(θ)的大致图象:

故选:D.
点评:此题考查了圆的标准方程,利用了数形结合的思想,弄清题意是解本题的关键.

练习册系列答案
相关题目
设P为曲线C:y=x2-x+3上的点,且曲线C在点P处切线斜率的取值范围为[0,1],则点P横坐标的取值范围为( )
A、[-1,-
| ||
| B、[-1,0] | ||
| C、[0,1] | ||
D、[
|
已知△ABC,点M在边BC上,且
=
,过M作GH分别与射线AB,AC交于G,H,且
=λ
,
=μ
,则λ+μ的最小值是( )
| BM |
| 1 |
| 2 |
| MC |
| AG |
| AB |
| AH |
| AC |
A、1+
| ||||
B、3+2
| ||||
C、
| ||||
D、1-
|
若函数f(x)=lnx,则f′(1)等于( )
| A、2 | B、1 | C、e | D、0 |
 已知,如图,四边形ABCD是平行四边形,点E是线段AB的中点,AC∩BD=O,点P是平面ABCD外一点,PA=PC,PB=PD,BD⊥EO.
已知,如图,四边形ABCD是平行四边形,点E是线段AB的中点,AC∩BD=O,点P是平面ABCD外一点,PA=PC,PB=PD,BD⊥EO.