题目内容
4. 如图,AB是半圆O的直径,点P为半圆O外一点,PA,PB分别交半圆O于点D,C.若AD=2,PD=4,PC=3,求BD的长.
如图,AB是半圆O的直径,点P为半圆O外一点,PA,PB分别交半圆O于点D,C.若AD=2,PD=4,PC=3,求BD的长.
分析 由切割线定理得:PD•PA=PC•PB,求出BC,利用勾股定理,求BD的长.
解答 解:由切割线定理得:PD•PA=PC•PB
则4×(2+4)=3×(3+BC),解得BC=5,…(4分)
又因为AB是半圆O的直径,故$∠ADB=\frac{π}{2}$,…(6分)
则在三角形PDB中有$BD=\sqrt{P{B^2}-P{D^2}}=\sqrt{64-16}=4\sqrt{3}$.…(10分)
点评 本题考查切割线定理的运用,考查勾股定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.在{1,3,5}和{2,4}两个集合中各取一个数组成一个两位数,则这个数能被4整除的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
13.已知向量$\vec a,\vec b$满足$|\vec a|=2$,$|\vec b|=\sqrt{3}$,且$\vec a$与$\vec b$夹角为30°,那么$\vec a•\vec b$等于( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | $3\sqrt{3}$ |
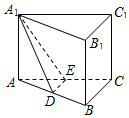 如图,在直三棱柱ABC-A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.
如图,在直三棱柱ABC-A1B1C1中,BC⊥AC,D,E分别是AB,AC的中点.