题目内容
15.所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数(也称为完备数、玩美数),如6=1+2+3;28=1+2+4+7+14;496=1+2+4+8+16+31+62+124+248,此外,它们都可以表示为2的一些连续正整数次幂之和,如6=21+22,28=22+23+24,…,按此规律,8128可表示为26+27+…+212.分析 依据定义,结合可以表示为2的一些连续正整数次幂之和,即可得出结论.
解答 解:由题意,2n-1是质数,2n-1(2n-1)是完全数,
∴令n=7,可得一个四位完全数为64×(127-1)=8128,
∴8128=26+27+…+212,
故答案为:26+27+…+212.
点评 本题考查合情推理,考查学生分析解决问题的能力,正确理解新定义是关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
10.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 6 | B. | $\frac{20}{3}$ | C. | 7 | D. | $\frac{22}{3}$ |
5.如果圆C:(x-a)2+(y-3)2=5的一条切线的方程为y=2x,那么a的值为( )
| A. | 4或1 | B. | -1或4 | C. | 1或-4 | D. | -1或-4 |
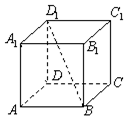 如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,
如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F, 如图,AB是半圆O的直径,点P为半圆O外一点,PA,PB分别交半圆O于点D,C.若AD=2,PD=4,PC=3,求BD的长.
如图,AB是半圆O的直径,点P为半圆O外一点,PA,PB分别交半圆O于点D,C.若AD=2,PD=4,PC=3,求BD的长.