题目内容
14．设等差数列{an}的公差是d，前n项和是Sn，若a1=1，a5=9，则公差d=2，Sn=n2．分析 利用等差数列的通项公式列出方程组，求出公差，由此能求出结果．
解答 解：∵等差数列{an}的公差是d，前n项和是Sn，a1=1，a5=9，
∴a5=a1+4d=1+4d=9，
解得公差d=2．
∴${S}_{n}=n{a}_{1}+\frac{n（n-1）}{2}d$=n+$\frac{n（n-1）}{2}×2$=n2．
故答案为：2，n2．
点评 本题考查等差数列的公差和前n项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
如图，AB是半圆O的直径，点P为半圆O外一点，PA，PB分别交半圆O于点D，C．若AD=2，PD=4，PC=3，求BD的长．
5．如果圆C：（x-a）2+（y-3）2=5的一条切线的方程为y=2x，那么a的值为（ ）
| A． | 4或1 | B． | -1或4 | C． | 1或-4 | D． | -1或-4 |
2．
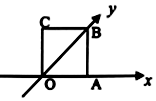如图水平放置的一个平面图形的直观图是边长为1cm的正方形，则原图形的周长是（ ）
如图水平放置的一个平面图形的直观图是边长为1cm的正方形，则原图形的周长是（ ）| A． | 8cm | B． | 6cm | C． | $2（1+\sqrt{3}）cm$ | D． | $2（1+\sqrt{2}）cm$ |
19．若复数z满足（1+i）z=i（i是虚数单位），则z的虚部为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$i | D． | -$\frac{1}{2}i$ |
60名学生某次数学考试成绩（单位：分）的频率分布直方图如图所示，则成绩不低于80分的学生人数是24．