题目内容
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙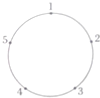 按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
 按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )| A、1 | B、2 | C、3 | D、4 |
考点:进行简单的合情推理
专题:规律型
分析:根据题意,分析可得青蛙的跳动规律为5-1-2-4-1-2,周期为3;又由2014=3×671+1,经过2014次跳后它停在的点所对应的数为1.
解答:
解:由5起跳,5是奇数,沿顺时针下一次只能跳一个点,落在1上.
由1起跳,1是奇数,沿顺时针下一次只能跳一个点,落在2上
2是偶数,沿顺时针跳两个点,落在4上.
由4起跳,是偶数,沿顺时针跳两个点,落在1上.
5-1-2-4-1-2,周期为3;又由2014=3×671+1,
∴经过2014次跳后它停在的点所对应的数为1.
故选A.
由1起跳,1是奇数,沿顺时针下一次只能跳一个点,落在2上
2是偶数,沿顺时针跳两个点,落在4上.
由4起跳,是偶数,沿顺时针跳两个点,落在1上.
5-1-2-4-1-2,周期为3;又由2014=3×671+1,
∴经过2014次跳后它停在的点所对应的数为1.
故选A.
点评:本题考查归纳推理、数列的性质和应用,解题时要审题,仔细求解.

练习册系列答案
相关题目
在三角形ABC中,A、B、C的对应边分别是a、b、c,若acosC=ccosA,且a、b、c成等比,则三角形ABC是( )
| A、等边三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、钝角三角形 |
已知曲线C1的参数方程
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系曲线,C2的极坐标方程为ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,
).设P为C1上任意一点,则|PA|2+|PB|2+|PC|2+|PD|2的取值范围是( )
|
| π |
| 3 |
| A、[12,52] |
| B、[32,52] |
| C、[12,32] |
| D、[20,32] |
已知函数f(x)的定义域为(0,+∞),若y=
在(0,+∞)上为增函数,则称f(x)为“一阶比增函数”;若y=
在(0,+∞)上为增函数,则称f(x)为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为Ω1,所有“二阶比增函数”组成的集合记为Ω2.若函数f(x)=x3-2hx2-hx,且f(x)∈Ω1,f(x)∉Ω2,则实数h的取值范围是( )
| f(x) |
| x |
| f(x) |
| x2 |
| A、[0,+∞) |
| B、(0,+∞) |
| C、(-∞,0] |
| D、(-∞,0) |
已知向量
,
满足|
|=1,|
|=2,
与
的夹角为60°,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
| C、1 | ||
| D、3 |
已知关于x的不等式x2+ax+b<0的解集为{x|-3<x<2},则实数a,b的值分别为( )
| A、-1,6 | B、1,-6 |
| C、-1,-6 | D、1,6 |
若直线ax+by=1与圆x2+y2=1有两个公共点,则点P(a,b)与圆的位置关系是( )
| A、在圆上 | B、在圆外 |
| C、在圆内 | D、以上皆有可能 |