题目内容
在三角形ABC中，A、B、C的对应边分别是a、b、c，若acosC=ccosA，且a、b、c成等比，则三角形ABC是（ ）
| A、等边三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、钝角三角形 |
考点：余弦定理
专题：三角函数的求值
分析：已知等式利用正弦定理化简，变形后利用两角和与差的正弦函数公式化简，得到A=C，利用等角对等边得到a=c，再由a、b、c成等比，利用等比数列的性质列出关系式，把a=c代入得到三边长相等，即可确定出三角形形状．
解答：
解：已知等式利用正弦定理化简得：sinAcosC=sinCcosA，即sinAcosC-cosAsinC=sin（A-C）=0，
∴A=C，即a=c，
∵a，b，c成等比，
∴b2=ac=a2，即b=a，
∴a=b=c，
则△ABC为等边三角形，
故选：A．
∴A=C，即a=c，
∵a，b，c成等比，
∴b2=ac=a2，即b=a，
∴a=b=c，
则△ABC为等边三角形，
故选：A．
点评：此题考查了正弦定理，等比数列的性质，熟练掌握正弦定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知△ABC，
+
=λ（
+
），则该三角形的形状为（ ）
| AB |
| AC |
| ||
|
|
| ||
|
|
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
若（x-
）n的展开式中第3项与第7项的二项式系数相等，则该展开式中x2的系数为（ ）
| 1 |
| x |
| A、-210 | B、56 |
| C、-56 | D、210 |
cos15°的值是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知角θ的终边上有一点P（-4，3），则cosθ的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如图，圆周上按顺时针方向标有1，2，3，4，5五个点，一只青蛙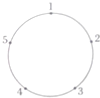
按顺时针方向绕圆周从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次跳两个点．该青蛙从5这个点跳起，经2014次跳后它将停在的点是（ ）
按顺时针方向绕圆周从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次跳两个点．该青蛙从5这个点跳起，经2014次跳后它将停在的点是（ ）| A、1 | B、2 | C、3 | D、4 |
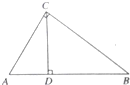如图，在△ABC中，∠ACB=90°，CD⊥AB，D为垂足，若CD=6cm，AD：DB=1：2，则AD的值是（ ）| A、6cm | ||
B、3
| ||
| C、18cm | ||
D、3
|