题目内容
已知函数f(x)的定义域为(0,+∞),若y=
在(0,+∞)上为增函数,则称f(x)为“一阶比增函数”;若y=
在(0,+∞)上为增函数,则称f(x)为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为Ω1,所有“二阶比增函数”组成的集合记为Ω2.若函数f(x)=x3-2hx2-hx,且f(x)∈Ω1,f(x)∉Ω2,则实数h的取值范围是( )
| f(x) |
| x |
| f(x) |
| x2 |
| A、[0,+∞) |
| B、(0,+∞) |
| C、(-∞,0] |
| D、(-∞,0) |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:因为f(x)∈Ω1且f(x)∉Ω2,即g(x)=
=x2-2hx-h在(0,+∞)是增函数,所以h≤0.而h(x)=
=x-
-2h在(0,+∞)不是增函数,而h′(x)=1+
,所以当h(x)是增函数时,有h≥0,所以当h(x)不是增函数时,有h<0.综上所述,可得h的取值范围是(-∞,0).
| f(x) |
| x |
| f(x) |
| x2 |
| h |
| x |
| h |
| x2 |
解答:
解:∵f(x)∈Ω1且f(x)∉Ω2,
即g(x)=
=x2-2hx-h在(0,+∞)是增函数,
∴h≤0.
而h(x)=
=x-
-2h在(0,+∞)不是增函数,
而h′(x)=1+
,
∴当h(x)是增函数时,有h≥0,
∴当h(x)不是增函数时,有h<0.
综上所述,可得h的取值范围是(-∞,0);
故选:D.
即g(x)=
| f(x) |
| x |
∴h≤0.
而h(x)=
| f(x) |
| x2 |
| h |
| x |
而h′(x)=1+
| h |
| x2 |
∴当h(x)是增函数时,有h≥0,
∴当h(x)不是增函数时,有h<0.
综上所述,可得h的取值范围是(-∞,0);
故选:D.
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
相关题目
若(x-
)n的展开式中第3项与第7项的二项式系数相等,则该展开式中x2的系数为( )
| 1 |
| x |
| A、-210 | B、56 |
| C、-56 | D、210 |
已知角θ的终边上有一点P(-4,3),则cosθ的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
函数f(x)=ax3+x恰有三个单调区间,则a的取值范围是( )
A、(-∞,-
| ||
B、[-
| ||
| C、[0,+∞) | ||
| D、(-∞,0) |
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙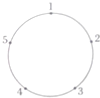 按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
 按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )| A、1 | B、2 | C、3 | D、4 |
函数f(x)=
在[-2,2]上的最大值为1,则实数a的取值范围是( )
|
| A、[0,+∞) |
| B、[0,e] |
| C、(-∞,0] |
| D、(-∞,e] |
下列命题正确的是( )
| A、小于90°的角一定是锐角 | ||
| B、终边相同的角一定相等 | ||
C、终边落在直线y=
| ||
| D、α-β=kπ,k∈Z,则角α的正切值等于角β的正切值 |
正方体ABCD-A1B1C1D1中,M,N分别为AB,DC中点,则直线MC与D1N所成角的余弦值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|