题目内容
已知向量
，
满足|
|=1，|
|=2，
与
的夹角为60°，则|
-
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
| C、1 | ||
| D、3 |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：由题意利用两个向量的数量积的定义可得
•
=1，再根据|
-
|=
=
，计算求得结果．
| a |
| b |
| a |
| b |
(
|
|
解答：
解：由题意可得
•
=1×2×cos60°=1，
∴|
-
|=
=
=
=
，
故选：A．
| a |
| b |
∴|
| a |
| b |
(
|
|
| 1-2+4 |
| 3 |
故选：A．
点评：本题主要考查两个向量的数量积的定义，求向量的模的方法，属于基础题．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
cos15°的值是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
某程序框图如图所示，现输入四个函数，则可输出的函数是（ ）
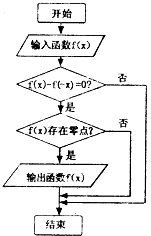
| A、f（x）=ex |
| B、f（x）=x2+2 |
| C、f（x）=2x+2-x |
| D、f（x）=log2|x| |
如图，圆周上按顺时针方向标有1，2，3，4，5五个点，一只青蛙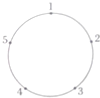
按顺时针方向绕圆周从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次跳两个点．该青蛙从5这个点跳起，经2014次跳后它将停在的点是（ ）
按顺时针方向绕圆周从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次跳两个点．该青蛙从5这个点跳起，经2014次跳后它将停在的点是（ ）| A、1 | B、2 | C、3 | D、4 |
设[x]表示不大于x的最大整数，则函数f（x）=lg2x-[lgx]-2的零点个数是（ ）
| A、4 | B、3 | C、2 | D、1 |
将自然数的前5个数：（1）排成1，2，3，4，5；（2）排成5，4，3，2，1；（3）排成2，1，5，3，4；（4）排成4，1，5，3，2．那么，可以叫做数列的只有（ ）
| A、（1） |
| B、（1），（2） |
| C、（1），（2），（3） |
| D、（1），（2），（3），（4） |
停车站划出一排10个停车位置，今有6辆不同的车需要停放，若要求剩余的4个空车位连在一起，则不同的停车方法有（ ）
A、
| ||||
B、2
| ||||
C、6
| ||||
D、7
|
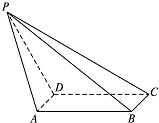如图，在四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PC=2