题目内容
已知曲线C1的参数方程
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系曲线,C2的极坐标方程为ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,
).设P为C1上任意一点,则|PA|2+|PB|2+|PC|2+|PD|2的取值范围是( )
|
| π |
| 3 |
| A、[12,52] |
| B、[32,52] |
| C、[12,32] |
| D、[20,32] |
考点:参数方程化成普通方程,两点间的距离公式
专题:选作题,坐标系和参数方程
分析:确定点A,B,C,D的直角坐标,利用参数方程设出P的坐标,借助于三角函数,即可求得|PA|2+|PB|2+|PC|2+|PD|2的取值范围.
解答:
解:点A,B,C,D的直角坐标为(1,
),(-
,1),(-1,-
),(
,-1),
设P(x0,y0),则
(φ为参数)
t=|PA|2+|PB|2+|PC|2+|PD|2=4x02+4y02+16=32+20sin2φ
∵sin2φ∈[0,1]
∴t∈[32,52].
故选:B.
| 3 |
| 3 |
| 3 |
| 3 |
设P(x0,y0),则
|
t=|PA|2+|PB|2+|PC|2+|PD|2=4x02+4y02+16=32+20sin2φ
∵sin2φ∈[0,1]
∴t∈[32,52].
故选:B.
点评:本题考查极坐标与直角坐标的互化,考查圆的参数方程的运用,属于中档题.

练习册系列答案
相关题目
已知△ABC,
+
=λ(
+
),则该三角形的形状为( )
| AB |
| AC |
| ||
|
|
| ||
|
|
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
cos15°的值是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知角θ的终边上有一点P(-4,3),则cosθ的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某程序框图如图所示,现输入四个函数,则可输出的函数是( )
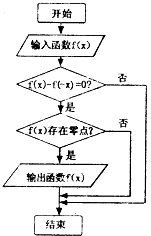

| A、f(x)=ex |
| B、f(x)=x2+2 |
| C、f(x)=2x+2-x |
| D、f(x)=log2|x| |
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙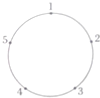 按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
 按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )
按顺时针方向绕圆周从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )| A、1 | B、2 | C、3 | D、4 |
将自然数的前5个数:(1)排成1,2,3,4,5;(2)排成5,4,3,2,1;(3)排成2,1,5,3,4;(4)排成4,1,5,3,2.那么,可以叫做数列的只有( )
| A、(1) |
| B、(1),(2) |
| C、(1),(2),(3) |
| D、(1),(2),(3),(4) |
如图,直线a在α内,b在β内,α⊥β,α∩β=c,∠1=∠2=60°则a、b所成角θ的余弦值为( )


| A、1 | ||
B、-
| ||
C、
| ||
D、
|