题目内容
已知关于x的不等式x2+ax+b＜0的解集为{x|-3＜x＜2}，则实数a，b的值分别为（ ）
| A、-1，6 | B、1，-6 |
| C、-1，-6 | D、1，6 |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：由不等式x2+ax+b＜0的解集，得出方程x2+ax+b=0的两实数根，由根与系数的关系求出a、b的值．
解答：
解：∵不等式x2+ax+b＜0的解集为{x|-3＜x＜2}，
∴方程x2+ax+b=0的两实数根是-3和2，
∴
；
解得a=1，b=-6．
故选：B．
∴方程x2+ax+b=0的两实数根是-3和2，
∴
|
解得a=1，b=-6．
故选：B．
点评：本题考查了一元二次不等式的解法与应用问题，解题时应结合不等式与对应的方程之间的关系，利用根与系数的关系，求出答案，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知角θ的终边上有一点P（-4，3），则cosθ的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如图，圆周上按顺时针方向标有1，2，3，4，5五个点，一只青蛙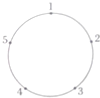
按顺时针方向绕圆周从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次跳两个点．该青蛙从5这个点跳起，经2014次跳后它将停在的点是（ ）
按顺时针方向绕圆周从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则下一次跳两个点．该青蛙从5这个点跳起，经2014次跳后它将停在的点是（ ）| A、1 | B、2 | C、3 | D、4 |
函数f（x）=
在[-2，2]上的最大值为1，则实数a的取值范围是（ ）
|
| A、[0，+∞） |
| B、[0，e] |
| C、（-∞，0] |
| D、（-∞，e] |
将自然数的前5个数：（1）排成1，2，3，4，5；（2）排成5，4，3，2，1；（3）排成2，1，5，3，4；（4）排成4，1，5，3，2．那么，可以叫做数列的只有（ ）
| A、（1） |
| B、（1），（2） |
| C、（1），（2），（3） |
| D、（1），（2），（3），（4） |
下列命题正确的是（ ）
| A、小于90°的角一定是锐角 | ||
| B、终边相同的角一定相等 | ||
C、终边落在直线y=
| ||
| D、α-β=kπ，k∈Z，则角α的正切值等于角β的正切值 |
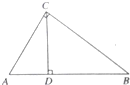如图，在△ABC中，∠ACB=90°，CD⊥AB，D为垂足，若CD=6cm，AD：DB=1：2，则AD的值是（ ）| A、6cm | ||
B、3
| ||
| C、18cm | ||
D、3
|
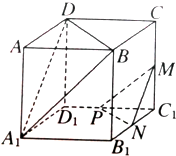在如图所示的正方体ABCD-A1B1C1D1中．