题目内容

4个人坐在一排7个座位上，问：
（1）空位不相邻的坐法有多少种；
（2）3个空位只有2个相邻的坐法有多少种；
（3）甲乙两人中间恰有2个空位的坐法有多少种？
考点：计数原理的应用
专题：排列组合
分析：（1）空位不相邻相当于将3个空位安插在4个人隔开的5个间隔中，问题得以解决．
（2）将相邻的2个空位当作一个元素，另一空位当作另一个元素，往5个间隔里插有A52种插法，问题得以解决．
（3）把甲乙两人和甲乙中间的2个空位当作一个元素，然后和另外2人和一个空位进行全排．根据分步计数原理得到结果．
解答： 解：4个人排有A44=24种，4人排好后包括两端共有5个“间隔”可以插入空位．
（1）空位不相邻相当于将4个空位安插在上述个“间隔”中，有C53=10种插法，
故空位不相邻的坐法有24×10=240种．
（2）把相邻的2个空位当作一个元素，另一空位当作另一个元素，往5个“间隔”里插
有A52种插法，故3个空位中只有2个相邻的坐法有A44A52=480种．
（3）把甲乙两人和甲乙中间的2个空位当作一个元素，然后和另外2人和一个空位进行全排，故有A21A44=48种
点评：本题考查插空法和捆绑法解决排列问题，相邻用捆绑，不相邻用插空，属于中档题．
练习册系列答案
相关题目
已知f（x）=x2，i是虚数单位，则在复平面中复数
f(1+i)
3+i
对应的点在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
已知在四棱锥E-ABCD中，底面ABCD是矩形，AB：BC=1：
2
，O、F分别为CD、BC的中点，且EO⊥平面ABCD，求证：AF⊥EF．
已知抛物线C：x2=2py（p＞0）的焦点为F，A，B为抛物线上异于坐标原点O的不同两点，抛物线C在A，B处的切线分别为l1，l2，且l1⊥l2，l1与l2相交于点D．
（Ⅰ）求点D的轨迹方程；
（Ⅱ）假设D点的坐标为（
3
2
，-1），问是否存在经过A，B两点且与l1，l2都相切的圆？若存在，求出该圆的方程；若不存在，请说明理由．
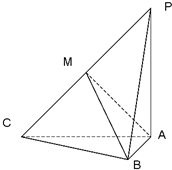如图，三棱锥P-ABC中，
PA
•
AB
=
PA
•
AC
=
AB
•
AC
=0，
PA
2=
AC
2=4
AB
2，M为棱PC的中点．
（I）求证：PC⊥平面MAB；
（Ⅱ）求二面角C-PB-A的余弦值．
在平面直角坐标系xoy中，以ox轴为始边做两个锐角α，β，它们的终边分别与单位圆相交于A，B两点，已知点A的横坐标为
2
10
，点B的纵坐标为
5
5
．
（1）求tan（α+β）的值；
（2）求α+2β的值．
已知函数f（x）=x-1-alnx，
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）若a＜0，对任意x1，x2∈（0，1]，且x1≠x2，都有|f（x1）-f（x2）|＜4|
1
x1
-
1
x2
|，求实数a的取值范围．
已知函数f（x）=-x+log2
1-x
1+x
．
（1）求f（
1
2013
）+f（-
1
2013
）的值；
（2）当x∈（-a，a]，其中a∈（0，1]，a是常数，函数f（x）是否存在最小值？若存在，求出f（x）的最小值；若不存在，请说明理由．
函数f（x）=x2+2x+5在[t，t+1]t∈R上的最小值为φ（t），求φ（t）的表达式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网