题目内容
在平面直角坐标系xoy中，以ox轴为始边做两个锐角α，β，它们的终边分别与单位圆相交于A，B两点，已知点A的横坐标为
，点B的纵坐标为
．
（1）求tan（α+β）的值；
（2）求α+2β的值．
| ||
| 10 |
| ||
| 5 |
（1）求tan（α+β）的值；
（2）求α+2β的值．
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：（1）由题意易得tanα=7，tanβ=
，由两角和的正切公式可得tan（α+β）；（2）由二倍角的正切公式可得tan2β，进而可得tan（α+2β），结合角的范围可得．
| 1 |
| 2 |
解答：
解：（1）由题意可得A的横坐标为
，纵坐标为
点B的纵坐标为
，横坐标为
，
∴tanα=7，tanβ=
，
∴tan（α+β）=
=-3
（2）由（1）可知tan2β=
=
，
∴tan（α+2β）=
=-1，
又∵α，β均为锐角，∴α+2β=
| ||
| 10 |
7
| ||
| 10 |
点B的纵坐标为
| ||
| 5 |
2
| ||
| 5 |
∴tanα=7，tanβ=
| 1 |
| 2 |
∴tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
（2）由（1）可知tan2β=
| 2tanβ |
| 1-tan2β |
| 4 |
| 3 |
∴tan（α+2β）=
| tanα+tan2β |
| 1-tanαtan2β |
又∵α，β均为锐角，∴α+2β=
| 3π |
| 4 |
点评：本题考查两角和与差的三角函数公式，涉及三角函数的定义，属基础题．
练习册系列答案
相关题目
直线l：3x-y-6=0被圆C：x2+y2-2x-4y=0截得的弦AB的长是（ ）
| A、10 | ||||
| B、5 | ||||
C、
| ||||
D、
|
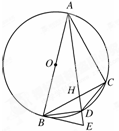如图，AB是⊙O的直径，BE为⊙O的切线，点C为⊙O上不同于A，B的一点，AD为∠BAC的平分线，且分别与BC交于H，与⊙O交于D，与BE交于E，连接BD，CD．