题目内容
20．求函数$f（x）={\frac{x}{3}^3}+{x^2}-3x-4在区间[{\left.{0，2}]}$上的单调区间，并求出该函数的最小值．分析 求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的最小值即可．
解答 解：f′（x）=x2+2x-3=（x+3）（x-1），
令f′（x）＞0，解得：x＞1或x＜-3，令f′（x）＜0，解得：-3＜x＜1，
故f（x）在[0，1）递减，在（1，2]递增，
故函数f（x）min=f（1）=-$\frac{17}{3}$．
点评 本题考查了函数的单调性、最值问题，考查导数的应用，是一道基础题．
练习册系列答案
相关题目
10．
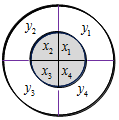已知两个半径不等的圆盘叠放在一起（有一轴穿过它们的圆心），两圆盘上分别有互相垂直的两条直径将其分为四个区域，小圆盘上所写的实数分别记为x1，x2，x3，x4，大圆盘上所写的实数分别记为y1，y2，y3，y4，如图所示．将小圆盘逆时针旋转i（i=1，2，3，4）次，每次转动90°，记Ti（i=1，2，3，4）为转动i次后各区域内两数乘积之和，例如T1=x1y2+x2y3+x3y4+x4y1．若x1+x2+x3+x4＜0，y1+y2+y3+y4＜0，则以下结论正确的是（ ）
已知两个半径不等的圆盘叠放在一起（有一轴穿过它们的圆心），两圆盘上分别有互相垂直的两条直径将其分为四个区域，小圆盘上所写的实数分别记为x1，x2，x3，x4，大圆盘上所写的实数分别记为y1，y2，y3，y4，如图所示．将小圆盘逆时针旋转i（i=1，2，3，4）次，每次转动90°，记Ti（i=1，2，3，4）为转动i次后各区域内两数乘积之和，例如T1=x1y2+x2y3+x3y4+x4y1．若x1+x2+x3+x4＜0，y1+y2+y3+y4＜0，则以下结论正确的是（ ）| A． | T1，T2，T3，T4中至少有一个为正数 | B． | T1，T2，T3，T4中至少有一个为负数 | ||
| C． | T1，T2，T3，T4中至多有一个为正数 | D． | T1，T2，T3，T4中至多有一个为负数 |