题目内容
在不等式组
,所表示的平面区域内任取一点P,若点P的坐标(x,y)满足y≥kx的概率为
,则实数k=( )
|
| 3 |
| 4 |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:由已知画出不等式组求出其对应的面积,即所有基本事件总数对应的几何量,再求出满足x-2y≤0区域的面积,代入几何概型计算公式,即可得到答案.
解答:
解:如图
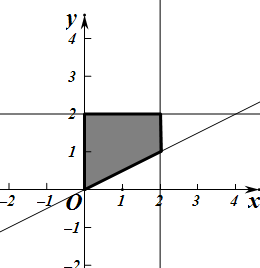
满足不等式组的区域是边长为2的正方形的面积为4,假设满足不等式y≥kx的区域如图阴影部分,其面积为4-
×2×2k,
由几何概型的概率公式得点P的坐标(x,y)满足y≥kx的概率为
=
,解得k=
.
故选D.
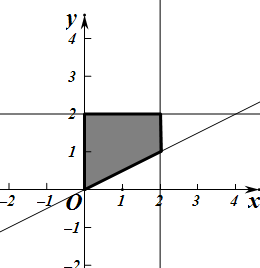
满足不等式组的区域是边长为2的正方形的面积为4,假设满足不等式y≥kx的区域如图阴影部分,其面积为4-
| 1 |
| 2 |
由几何概型的概率公式得点P的坐标(x,y)满足y≥kx的概率为
4-
| ||
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
故选D.
点评:本题考查的知识点是几何概型,二元一次不等式(组)与平面区域,求出满足条件A的基本事件对应的“几何度量”(长度、面积、体积),再求出总的基本事件对应的“几何度量”,最后根据概率公式求解.

练习册系列答案
相关题目
下列函数中,在其定义域内既是奇函数,又是减函数的是( )
| A、y=-x3 | ||
| B、y=sinx | ||
| C、y=tanx | ||
D、y=(
|
某项实验,要先后实施6个程序,其中程序A只能出现在第一或最后一步,程序B和C在实施时必须相邻,问实验顺序的编排方法共有( )
| A、34种 | B、48种 |
| C、96种 | D、144种 |

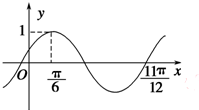 函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<