题目内容
已知函数f（x）=x3-mx2-x+1，其中m为实数．
（1）当m=1时，求函数f（x）在区间[-1，
]上的最大值和最小值；
（2）若对一切的实数x，有f′（x）≥|x|-
恒成立，其中f′（x）为f（x）的导函数，求实数m的取值范围．
（1）当m=1时，求函数f（x）在区间[-1，
| 4 |
| 3 |
（2）若对一切的实数x，有f′（x）≥|x|-
| 7 |
| 4 |
考点：利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题：分类讨论,导数的综合应用
分析：（1）利用导数数判断函数的单调性，利用单调性求出函数的极值和区间端点值，从而求出函数的最大值和最小值；
（2）分x＞0，x=0，x＜0三类进行讨论，分别求出在给定区间上的最值，解决恒成立问题．
（2）分x＞0，x=0，x＜0三类进行讨论，分别求出在给定区间上的最值，解决恒成立问题．
解答：
解：（1）∵当m=1时，f（x）=x3-x2-x+1，
∴f′（x）=3x2-2x-1=（x-1）（3x+1），
当x＜-
或x＞1时f′（x）＞0，当-
＜x＜1时，f′（x）＜0，
∴f（x）在[-1，-
）和（1，
]上单调递增，在（-
，1）上单调递减，
又f（-1）=0，f(-
)=
，f（1）=0，f(
)=
，
∴f（x）在区间上的最大值为f(-
)=
，最小值为f（1）=0；
（2）f′（x）=3x2-2mx-1⇒3x2-2mx-1≥|x|-
①当x=0时，m∈R；
②当x＞0时，3x2-(2m+1)x+
≥0⇒2m+1≤3(x+
)，在x＞0时恒成立，
∵3(x+
)min=3，此时x=
，∴2m+1≤3，∴m≤1；
③当x＜0时，3x2-(2m-1)x+
≥0即2m-1≥3(x+
)，在x＜0时恒成立，
∵3(x+
)max=-3，此时x=-
，∴2m-1≥-3，∴m≥-1；
综上得m的取值范围为[-1，1]．
∴f′（x）=3x2-2x-1=（x-1）（3x+1），
当x＜-
| 1 |
| 3 |
| 1 |
| 3 |
∴f（x）在[-1，-
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
又f（-1）=0，f(-
| 1 |
| 3 |
| 32 |
| 27 |
| 4 |
| 3 |
| 7 |
| 27 |
∴f（x）在区间上的最大值为f(-
| 1 |
| 3 |
| 32 |
| 27 |
（2）f′（x）=3x2-2mx-1⇒3x2-2mx-1≥|x|-
| 7 |
| 4 |
①当x=0时，m∈R；
②当x＞0时，3x2-(2m+1)x+
| 3 |
| 4 |
| 1 |
| 4x |
∵3(x+
| 1 |
| 4x |
| 1 |
| 2 |
③当x＜0时，3x2-(2m-1)x+
| 3 |
| 4 |
| 1 |
| 4x |
∵3(x+
| 1 |
| 4x |
| 1 |
| 2 |
综上得m的取值范围为[-1，1]．
点评：本题考查了利用导数判断函数的单调区间，从而求最值，利用最值解决恒成立问题，运用了分类讨论思想．是一道导数应用的综合题，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
曲线y=x3-2x+4在点（1，3）处的切线方程为（ ）
| A、3x-y=0 |
| B、x+y-4=0 |
| C、x-y+2=0 |
| D、x-y-2=0 |
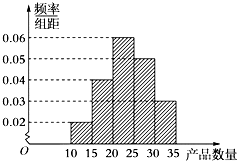为了调查某厂2000名工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35]，频率分布直方图如图所示．工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训，则这2位工人不在同一组的概率是（ ）
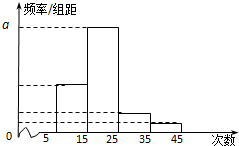对某校高二年级学生中学阶段参加社区服务的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图，