题目内容
曲线y=x3-2x+4在点（1，3）处的切线方程为（ ）
| A、3x-y=0 |
| B、x+y-4=0 |
| C、x-y+2=0 |
| D、x-y-2=0 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求出函数y=x3-2x+4的导函数，然后求出在x=1处的导数，从而求出切线的斜率，利用点斜式方程求出切线方程即可．
解答：
解：y'=3x2-2，
∴y'|x=1=3-2=1，又切点为（1，3），
∴曲线y=x3-2x+4在点（1，3）处的切线方程为x-y+2=0，
故选C．
∴y'|x=1=3-2=1，又切点为（1，3），
∴曲线y=x3-2x+4在点（1，3）处的切线方程为x-y+2=0，
故选C．
点评：本题主要考查了利用导数研究曲线上某点切线方程，考查运算求解能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知（1+x）6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6，则a1+a3+a5=（ ）
| A、-16 | B、0 | C、16 | D、32 |
在△ABC中，若cosBsinC=sinA，则△ABC的形状一定是（ ）
| A、等腰直角三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等边三角形 |
已知α=
π，则角α的终边所在的象限是（ ）
| 28 |
| 9 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知θ为第一象限角，若将角θ的终边逆时针旋转
，则它与单位圆的交点坐标是（ ）
| π |
| 2 |
| A、（cosθ，sinθ） |
| B、（cosθ，-sinθ） |
| C、（sinθ，-cosθ） |
| D、（-sinθ，cosθ） |
执行如图所示的程序框图，若输入n的值为4，则输出S的值为（ ）
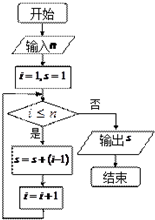
| A、5 | B、6 | C、7 | D、8 |