题目内容
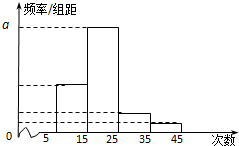 对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,
对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,| 分组 | 频数 | 频率 |
| [5,15) | 10 | 0.25 |
| [15,25) | 26 | 0.65 |
| [25,35) | 3 | P |
| [35,45) | m | 0.025 |
| 合计 | M | 1 |
(Ⅱ)请根据频率分布直方图估计这M名学生参加社区服务的次数的众数与中位数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于25次的学生中任选2人,求恰有一人参加社区服务次数落在区间[35,45)内的概率.
考点:古典概型及其概率计算公式,频率分布直方图,众数、中位数、平均数
专题:概率与统计
分析:(I)利用[15,25)内的频数是26,频率是0.65,求出样本的容量,再利用频数之和为样本容量,频率之和为1,求M,m,P及a值;
(II)M名学生参加社区服务的次数的众数约为频率最高组的组中值,中位数为平分概率分布直方图的值;
(III)求出参加社区服务次数不少于25次的学生数,写出任选2人的所有基本事件,找出恰有一人参加社区服务次数在区间[35,45)内的基本事件,代入概率公式计算.
(II)M名学生参加社区服务的次数的众数约为频率最高组的组中值,中位数为平分概率分布直方图的值;
(III)求出参加社区服务次数不少于25次的学生数,写出任选2人的所有基本事件,找出恰有一人参加社区服务次数在区间[35,45)内的基本事件,代入概率公式计算.
解答:
解:(Ⅰ)由分组[15,25)内的频数是26,频率是0.65知,
=0.65,所以M=40,
因为频数之和为40,所以10+26+3+m=40,m=1,
p=
=
=0.075,
因为a是对应分组[15,25)的频率与组距的商,
所以a=
=0.13;
(Ⅱ)M名学生参加社区服务次数的众数为频率最高组的组中值,
即[15,25)的组中值,
故M名学生参加社区服务次数的众数约为20,
又∵[5,15)的频率为0.25<0.5,
[5,25)的累积频率为0.25+0.65>0.5,
故M名学生参加社区服务次数的中位数约为15+
×10≈18.85,即19次,
(Ⅲ)这个样本中,参加社区服务次数不少于25次的学生共有m+3=4人
设在区间[25,35)内的人为a1,a2,a3,在区间[35,45)内的人为b,
则任选2人共6种情况:
(a1,a2),(a1,a3),(a2,a3),(a1,b),(a2,b),(a3,b),
恰有一人参加社区服务次数在区间[25,30)内的情况共有3种:(a1,b),(a2,b),(a3,b),
所以,恰有一人参加社区服务次数在区间M内的概率为p=
=
.
| 26 |
| M |
因为频数之和为40,所以10+26+3+m=40,m=1,
p=
| 3 |
| M |
| 3 |
| 40 |
因为a是对应分组[15,25)的频率与组距的商,
所以a=
| 0.65 |
| 5 |
(Ⅱ)M名学生参加社区服务次数的众数为频率最高组的组中值,
即[15,25)的组中值,
故M名学生参加社区服务次数的众数约为20,
又∵[5,15)的频率为0.25<0.5,
[5,25)的累积频率为0.25+0.65>0.5,
故M名学生参加社区服务次数的中位数约为15+
| 0.25 |
| 0.65 |
(Ⅲ)这个样本中,参加社区服务次数不少于25次的学生共有m+3=4人
设在区间[25,35)内的人为a1,a2,a3,在区间[35,45)内的人为b,
则任选2人共6种情况:
(a1,a2),(a1,a3),(a2,a3),(a1,b),(a2,b),(a3,b),
恰有一人参加社区服务次数在区间[25,30)内的情况共有3种:(a1,b),(a2,b),(a3,b),
所以,恰有一人参加社区服务次数在区间M内的概率为p=
| 3 |
| 6 |
| 1 |
| 2 |
点评:本题考查了由频率分布直方图求平均数,考查了古典概型的概率计算,考查了学生的读图努力与数据处理能力,读懂频率分布表是关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知α=
π,则角α的终边所在的象限是( )
| 28 |
| 9 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
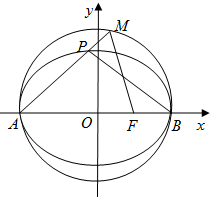 已知椭圆C:
已知椭圆C: