��Ŀ����
��֪˫����C��������ԭ���Ҿ�����D��2��0����
=��2��1����
=��2��-1���ֱ������������ߵķ���������
��1����˫����C�ķ��̣�
��2����Բ
+y2=1����ΪA������B��-
��0����ֱ��?����Բ����M��N���㣬���ж�
•
�Ƿ�Ϊ��ֵ����֤����Ľ��ۣ�
��3��˫����C��������y2=2px��p��0���Ƿ�Ҳ�����ƣ�2���Ľ��ۣ����ǣ���ѡ��һ������д�����ƽ��ۣ���Ҫ����д����֤�����̣���
| m1 |
| m2 |
��1����˫����C�ķ��̣�
��2����Բ
| x2 |
| 4 |
| 6 |
| 5 |
| AM |
| AN |
��3��˫����C��������y2=2px��p��0���Ƿ�Ҳ�����ƣ�2���Ľ��ۣ����ǣ���ѡ��һ������д�����ƽ��ۣ���Ҫ����д����֤�����̣���
���㣺ֱ����Բ���ߵ��ۺ�����,�������,˫���ߵı�����
ר�⣺Բ�����е���ֵ�뷶Χ����
��������1�����˫���ߵĽ����߷��̣����a��b�����ɵõ�˫����C�ķ��̣�
��2���ж�
•
�Ƿ�Ϊ��ֵ��ͨ��ֱ��?��б�ʲ�����ʱ��ֱ���ж���⣮ֱ��?��б�ʴ���ʱ�����ֱ�߷�����˫���߷���������ͨ��Τ�ﶨ���Լ������������������������ɣ�
��3��˫����C��������y2=2px��p��0��Ҳ�����ƣ�2���Ľ��ۣ�д�����ƽ��ۣ���Ҫ����д����֤�����̣���
��2���ж�
| AM |
| AN |
��3��˫����C��������y2=2px��p��0��Ҳ�����ƣ�2���Ľ��ۣ�д�����ƽ��ۣ���Ҫ����д����֤�����̣���
���
�⣺��1�����������ߵķ���Ϊy=��
x��������a=2������b=1����˫����C�ķ���Ϊ��
-y2=1����3��
��2��
•
Ϊ��ֵ0���������£���ֱ��?��б�ʲ�����ʱ��?�ķ���Ϊx=-
�����M(-
��
)��N(-
��-
)����ʱ
•
=(
��
)•(
��-
)=0����4��
��ֱ��?��б�ʴ���ʱ����ֱ��?�ķ���Ϊ��y=k(x+
)��
����
�ã�100k2+25��x2+240k2x+144k2-100=0��
��Ȼ����0��
��M��x1��y1����N��x2��y2������
����6�䣬
y1•y2=k2(x1+
)(x2+
)=k2[x1•x2+
(x1+x2)+
]=-
��
����
•
=(x1+2��y1)•(x2+2��y2)=(x1+2)•(x2+2)+y1•y2=x1•x2+2(x1+x2)+4+y1•y2��9��
=
+2(-
)+4+
=0��
����������
•
Ϊ��ֵ0����10��
��3��˫����C��
-y2=1����ΪA������B(-
��0)��ֱ��?��˫����C����M��N���㣬
��
•
Ϊ��ֵ0��
˵�����ٱ���ָ��B�����꣬�����Բ�˵���嶨ֵ��
�ڶ�˫����C���ԣ����Ҷ�����صĵ�ΪB(
��0)��
��������y2=2px��p��0��Ҳ�����ƽ��ۣ�������y2=2px��p��0���Ķ���ΪO��������B��2p��0����ֱ��?��������y2=2px��p��0������M��N���㣬��
•
Ϊ��ֵ0����13��
| 1 |
| 2 |
| x2 |
| 4 |
��2��
| AM |
| AN |
| 6 |
| 5 |
| 6 |
| 5 |
| 4 |
| 5 |
| 6 |
| 5 |
| 4 |
| 5 |
| AM |
| AN |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
��ֱ��?��б�ʴ���ʱ����ֱ��?�ķ���Ϊ��y=k(x+
| 6 |
| 5 |
����
|
��Ȼ����0��
��M��x1��y1����N��x2��y2������
|
y1•y2=k2(x1+
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 36 |
| 25 |
| 64k2 |
| 100k2+25 |
����
| AM |
| AN |
=
| 144k2-100 |
| 100k2+25 |
| 240k2 |
| 100k2+25 |
| -64k2 |
| 100k2+25 |
����������
| AM |
| AN |
��3��˫����C��
| x2 |
| 4 |
| 10 |
| 3 |
��
| AM |
| AN |
˵�����ٱ���ָ��B�����꣬�����Բ�˵���嶨ֵ��
�ڶ�˫����C���ԣ����Ҷ�����صĵ�ΪB(
| 10 |
| 3 |
��������y2=2px��p��0��Ҳ�����ƽ��ۣ�������y2=2px��p��0���Ķ���ΪO��������B��2p��0����ֱ��?��������y2=2px��p��0������M��N���㣬��
| AM |
| AN |
���������⿼��ֱ����Բ���ߵ��ۺ�Ӧ�ã�˫���߷��̵������������Ӧ�ã��ۺ��ԱȽ�ǿ��

��ϰ��ϵ�д�
�����Ŀ
ִ����ͼ��ʾ�ij����ͼ��������n��ֵΪ4�������S��ֵΪ��������
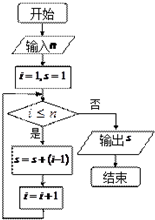

| A��5 | B��6 | C��7 | D��8 |
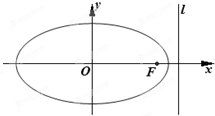 ��ԲC���ҽ���ΪF������Ϊl��������Ϊ
��ԲC���ҽ���ΪF������Ϊl��������Ϊ