题目内容
某商品进价为每件8元,若按每件10元出售可销售100件,若售价每增加1元,则日销量减少10件,问商品售价为 元时,每天所赚的利润最大.
考点:函数最值的应用
专题:函数的性质及应用
分析:(1)题中等量关系为:利润=(售价-进价)×售出件数,根据等量关系列出函数关系式;
(2)将(1)中的函数为一元二次函数,把关系式配方,根据配方后的方程式即可求出y的最大值
(2)将(1)中的函数为一元二次函数,把关系式配方,根据配方后的方程式即可求出y的最大值
解答:
解:(1)∵利润=(售价-进价)×售出件数,设商品售价为x元,
∴y=(x-8)[100-10(x-10)],
即y=-10x2+280x-1600(10≤x≤20);
(2)将(1)中方程式配方得:
y=-10(x-14)2+360,
∴当x=14时,y最大=360元,
答:售价为14元时,利润最大.
∴y=(x-8)[100-10(x-10)],
即y=-10x2+280x-1600(10≤x≤20);
(2)将(1)中方程式配方得:
y=-10(x-14)2+360,
∴当x=14时,y最大=360元,
答:售价为14元时,利润最大.
点评:本题主要考查对与二次函数的应用,根据题意,找好题中的等量关系,列出函数表达式,再求函数的最值.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
若2014a=
,2014b=3,则a+2b等于( )
| 2014 |
| 9 |
| A、0 | B、1 | C、2 | D、3 |
集合M={x|x=
±45°,k∈z},P={x|x=
±90°,k∈Z},则M、P之间的关系为( )
| k•180° |
| 2 |
| k•180° |
| 4 |
| A、M=P | B、M⊆P? |
| C、M?P | D、M∩P=∅ |
等比数列{an}中,已知a3•a10=8a52,a2=2,则a1=( )
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
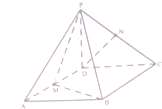 已知四棱锥P-ABCD,底面ABCD是∠A=60°,边长为a的菱形,又PD⊥底面ABCD,且PD=CD,点M,N分别是棱AD,PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°,边长为a的菱形,又PD⊥底面ABCD,且PD=CD,点M,N分别是棱AD,PC的中点.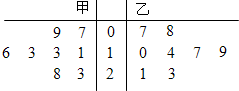 某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响.
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响. 已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,则a-b的值为
已知函数f(x)=ax+b(a>0,a≠1)的图象如图所示,则a-b的值为