题目内容
已知函数f(x)=log2
.
(1)求证:f(x1)+f(x2)=f(
);
(2)若f(
)=1,f(-b)=
,求f(a)的值.
| 1+x |
| 1-x |
(1)求证:f(x1)+f(x2)=f(
| x1+x2 |
| x1x2 |
(2)若f(
| a+b |
| 1+ab |
| 1 |
| 2 |
考点:对数的运算性质
专题:计算题
分析:(1)分别表示出f(x1),f(x2),f(
);即可证出等式;
(2)由f(
)=1表示出a,由f(-b)=
求出值,求出a值,代入求出f(a).
| x1+x2 |
| x1x2 |
(2)由f(
| a+b |
| 1+ab |
| 1 |
| 2 |
解答:
解:(1)∵f(x)=log2
,
∴f(x1)+f(x2)=log2
+log2
=log2
•
=log2
f(
)=log2
=log2
,
∴f(x1)+f(x2)=f(
);
(2)∵f(
)=1,
∴
=2,
∴a=
,
∵f(-b)=
,
∴log2
=
,解得b=2
-3,
∴a=
=
∴f(a)=log2
=log2
=log22
=
| 1+x |
| 1-x |
∴f(x1)+f(x2)=log2
| 1+x1 |
| 1-x1 |
| 1+x2 |
| 1-x2 |
=log2
| 1+x1 |
| 1-x1 |
| 1+x2 |
| 1-x2 |
| x1x2+x1+x2 |
| x 1x2-x1-x2 |
f(
| x1+x2 |
| x1x2 |
1+
| ||
1-
|
| x1x2+x1+x2 |
| x 1x2-x1-x2 |
∴f(x1)+f(x2)=f(
| x1+x2 |
| x1x2 |
(2)∵f(
| a+b |
| 1+ab |
∴
1+
| ||
1-
|
∴a=
| 1-3b |
| 3-b |
∵f(-b)=
| 1 |
| 2 |
∴log2
| 1-b |
| 1+b |
| 1 |
| 2 |
| 2 |
∴a=
1-3(2
| ||
3-(2
|
5-3
| ||
3-
|
∴f(a)=log2
| 1+a |
| 1-a |
1+
| ||||||
1-
|
| 2 |
| 3 |
| 2 |
点评:本题考查对数的运算法则及运算能力,属于一道中档题.

练习册系列答案
相关题目
函数f(x)=x3-x+1的零点所在区间是( )
| A、(-3,-2) |
| B、(-2,-1) |
| C、(-1,0) |
| D、(0,1) |
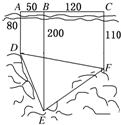 如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,则∠DEF的余弦值为( )
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC=120m,于A处测得水深AD=80m,于B处测得水深BE=200m,于C处测得水深CF=110m,则∠DEF的余弦值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
设θ是第二象限角,且sin
+cos
<0,则sin
,cos
,tan
的大小关系是( )
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
A、sin
| ||||||
B、cos
| ||||||
C、sin
| ||||||
D、tan
|
已知a=3-
,b=log2
,c=log
,则( )
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、c>b>a |