题目内容
两圆ρ=2cosθ,ρ=2sinθ的公共部分面积是( )
A、
| ||||
| B、π-2 | ||||
C、
| ||||
D、
|
考点:圆与圆的位置关系及其判定
专题:数形结合
分析:把两圆的极坐标方程分别化为普通方程,在坐标系中画出图形,找出两圆的公共部分为如图所示的阴影部分,且四边形AOBC为边长是1的正方形,然后由半圆的面积减去正方形的面积即可求出阴影部分面积即为两圆的公共部分面积.
解答:
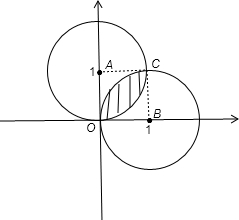 解:把两圆的极坐标方程分别化为普通方程得:
解:把两圆的极坐标方程分别化为普通方程得:
(x-1)2+y2=1,x2+(y-1)2=1,
画出图形,两圆的公共部分为阴影部分,如图所示:
根据题意得到四边形AOBC为边长为1的正方形,
则S阴影=S半圆-S正方形=
-1.
故选C
 解:把两圆的极坐标方程分别化为普通方程得:
解:把两圆的极坐标方程分别化为普通方程得:(x-1)2+y2=1,x2+(y-1)2=1,
画出图形,两圆的公共部分为阴影部分,如图所示:
根据题意得到四边形AOBC为边长为1的正方形,
则S阴影=S半圆-S正方形=
| π |
| 2 |
故选C
点评:此题考查了极坐标与平面直角坐标的互化,以及两圆的位置关系,考查了数形结合的思想.画出图形得到阴影部分即为两圆的公共部分是解本题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
在极坐标系中,圆ρ=2cosθ的圆心到直线ρcos(θ-
)=1的距离是( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |