题目内容
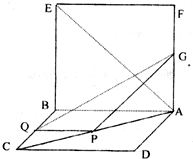 如图,在直二面角E-AB-C中,四边形ABCD和四边形ABEF都是矩形,AB=AF=4,AD=2,点P、Q、G分别是AC、BC、AF的中点;
如图,在直二面角E-AB-C中,四边形ABCD和四边形ABEF都是矩形,AB=AF=4,AD=2,点P、Q、G分别是AC、BC、AF的中点;(Ⅰ)求FB与PG所成角的正切值:
(Ⅱ)求二面角G-PQ-A,的平面角的正切值.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:计算题
分析:(I)取AB的中点为M,又G为AF的中点,由三角形中位线定理得GM∥BF,则∠PGM是FB与PG所成角,由已知中直二面角E-AB-C中,四边形ABCD和四边形ABEF都是矩形,AB=AF=4,AD=2,解△PMG即可得到FB与PG所成角的正切值:
(Ⅱ)延长QP交AD于K,由面面垂直的性质定理,结合二面角E-AB-C为直二面角,易得QK⊥GK而AK⊥QK,即∠GKA是二面角G-PQ-A的平面角,解Rt△AKG,即可得到二面角G-PQ-A,的平面角的正切值.
(Ⅱ)延长QP交AD于K,由面面垂直的性质定理,结合二面角E-AB-C为直二面角,易得QK⊥GK而AK⊥QK,即∠GKA是二面角G-PQ-A的平面角,解Rt△AKG,即可得到二面角G-PQ-A,的平面角的正切值.
解答:
 解:(I)取AB的中点为M,又G为AF的中点,则GM∥BF
解:(I)取AB的中点为M,又G为AF的中点,则GM∥BF
所以∠PGM是FB与PG所成角(3分)
由PM∥AD,AD⊥AB知PM⊥AB
又二面角E-AB-C是直二面角
即中平面ABCD⊥平面ABEF,交线是AB,
所以PM⊥平面ABEF,
所以PM⊥MG于是△PMG是直角三角形,
PM=
AD=1
GM=
=2
,
∴tan∠PGM=
=
(7分)
(Ⅱ)延长QP交AD于K,由平面ABCD⊥平面ABEF,AG⊥AB知AG⊥平面ABCD,
又QK⊥AD
∴QK⊥GK而AK⊥QK,
所以∠GKA是二面角G-PQ-A的平面角.(10分)
则Rt△AKG中,AK=1,AG=2
∴tan∠GKA=2.(13分)
 解:(I)取AB的中点为M,又G为AF的中点,则GM∥BF
解:(I)取AB的中点为M,又G为AF的中点,则GM∥BF所以∠PGM是FB与PG所成角(3分)
由PM∥AD,AD⊥AB知PM⊥AB
又二面角E-AB-C是直二面角
即中平面ABCD⊥平面ABEF,交线是AB,
所以PM⊥平面ABEF,
所以PM⊥MG于是△PMG是直角三角形,
PM=
| 1 |
| 2 |
GM=
| AG2+AM2 |
| 2 |
∴tan∠PGM=
| PM |
| MG |
| ||
| 4 |
(Ⅱ)延长QP交AD于K,由平面ABCD⊥平面ABEF,AG⊥AB知AG⊥平面ABCD,
又QK⊥AD
∴QK⊥GK而AK⊥QK,
所以∠GKA是二面角G-PQ-A的平面角.(10分)
则Rt△AKG中,AK=1,AG=2
∴tan∠GKA=2.(13分)
点评:本题考查的知识点是二面角的平面角及求法,异面直线及其所成的角,其中(I)的关键是证得∠PGM是FB与PG所成角,而(II)的关键是证得∠GKA是二面角G-PQ-A的平面角.

练习册系列答案
相关题目
已知直线y=ex+1与曲线y=ex+a相切(e是自然对数的底数),则a的值是( )
| A、e | ||
B、
| ||
| C、e+1 | ||
| D、1 |
 如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.
如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.| A、504 | B、501 |
| C、500 | D、550 |
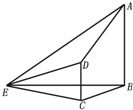 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.