题目内容
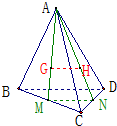
如图，A是平面BCD外的一点G，H分别是△ABC，△ACD的重心，求证：GH∥BD．
考点：三角形五心
专题：计算题
分析：连接AG并延长，交BC于M，连接AH并延长，交CD于N，由G，H分别是△ABC，△ACD的重心，知M，N分别是BC和CD的中点，由三角形中位线定理和平行公理能够证明GH∥BD．
解答：
证明：如图，连接AG并延长，交BC于M，
连接AH并延长，交CD于N，
∵G，H分别是△ABC，△ACD的重心，
∴M，N分别是BC和CD的中点，
∴BD∥MN
又∵
=
=2，
∴GH∥MN，
∴GH∥BD．
证明：如图，连接AG并延长，交BC于M，连接AH并延长，交CD于N，
∵G，H分别是△ABC，△ACD的重心，
∴M，N分别是BC和CD的中点，
∴BD∥MN
又∵
| AG |
| GM |
| AH |
| HN |
∴GH∥MN，
∴GH∥BD．
点评：本题考查三角形五心的性质和应用，是基础题．解题时要恰当地连接辅助线，合理利用三角形中位线定理和平行公理进行解题．易错点是不能恰当地作辅助线．
练习册系列答案
相关题目
抛物线y2=2px（p＞0）的焦点到双曲线
-
=1渐近线的距离为
，则实数p等于（ ）
| x2 |
| 4 |
| y2 |
| 12 |
| 3 |
| A、2 | B、4 | C、8 | D、16 |
已知直线y=ex+1与曲线y=ex+a相切（e是自然对数的底数），则a的值是（ ）
| A、e | ||
B、
| ||
| C、e+1 | ||
| D、1 |